神話的搖籃曲 - 平面神話秩序 (上)
數學家的墓碑
很久很久以前,有一個陌生的旅客路過一個地圖上沒有記載的小鎮,他在小鎮外的墓園看到三塊墓碑,墓碑上分別寫著︰
| 數學家的父親 ◭ | 數學家的母親 ◮ | 數學家女兒 ▲ |
墓碑前還有著祭拜的花,這些花還未枯萎。
作為一個對數學感興趣的人,路過的旅客拿起電話手機,在網絡上搜尋那位「數學家女兒」的數學成就。
然而他在網絡上卻甚麼都搜不到,在最先進的搜索引擎搜不到,向最先進的 AI 提問沒有得到答案,查詢所有學術論文庫也找不到這位「數學家女兒」的痕跡。
受數據荒蕪挫折的旅客決定進入小鎮,問一問當地老人知不知道這到底是甚麼一回事。

小鎮往事
這是一座平靜的小鎮,小鎮居民不富裕但生活安康。
小鎮的中心是一座神廟,旅客對神廟供奉的神明是哪一位一無所知。
他在神廟外的廣場,找到了位很老很老的老人,這位老人當時在喂白鴿。
旅客︰老人家,恕我冒昩打擾,不知道你對小鎮的過往是否熟悉?
老人︰你好陌生人,我在這座小鎮已生活了很久很久,對它大部份的過往都還留有記憶。
旅客︰我在小鎮外的墓園看到三塊墓碑,分別寫著「數學家的父親」「數學家的母親」和「數學家女兒」,請問老伯知不知道這一家人的過往?
老人︰當然,那家人的後代雖然已經不在這座小鎮生活,但他們的故事在我的腦海中留下了深刻的記憶。
老人的回憶
「數學家女兒」是那一家人最小的女兒,那家人的父母雖受的教育不多,但都是善良而勤勞的人,在鎮上有著很好的名聲。兩夫婦其他的子女都已成年,並去到不同的地方生活,沒想到臨老時卻再得到一個小女兒。
他們把小女兒視若珍寶,對她十分寵愛。
小女兒天生活潑,開朗樂觀,好動且充滿好奇心。
從小她就有一個夢想 - 成為像 希帕蒂婭 (Hypatia / Ὑπατία) [1] 那樣的哲學家、天文學家、數學家。
小女孩會想像希帕蒂婭在歷史上會是怎樣的,那時的人們的文化習俗,亞歷山大城的夜空是如何等等;她也會為希帕蒂婭的死亡而悲傷。

儘管小女兒的夢想是成為一名數學家,然而她的天賦卻似乎不在數學上,學校的數學考試她通常都只是僅僅合格。她花了很多時間提高自己的數學考試分數,卻收效甚微。
另一方面,小女兒有著明顯的音樂、語言與運動才能,她在小時候就被老師發現有絕對音感 (perfect pitch),對聽過一兩次的旋律過耳不忘,並能還原出曲譜。
每當女孩心情煩悶時,她就會一個人靜靜的看著星空,哼著她聽過的曲調。有時她會自己跳起舞來,旋轉又旋轉,直到頭暈目眩才停下來。

女孩仍未放棄她的數學夢想,她用她的零花錢買了一些與數學相關的書藉,其中一本她非常喜愛,常常和她的朋友分享裏面的故事。
這本故事書,名為《平面國》(Flatland) [2] [3] [4]。

旅客的恍惚
當聽到老人家提及《平面國》(Flatland) 這本書時,陌生的旅客意識進入了恍惚 (trance)。
旅客知道《平面國》,他也讀過,並記得這本書有幾部改編的電影,這本書出版於 1884 年。
這本的作者是 Edwin A. Abbott [5],生於 1838 年維多利亞時代的英國,在劍橋大學學習古典學 (classics)、數學、神學,是一名聖公會的神職人員,一生致力於教育與精神的追尋,喜好莎士比亞。

《平面國》這小故事的大概,是敍述一個生活在 二維平面世界 的 正方形 (阿方) 在新的千禧年 2000 年時,遇上了自稱來自 三維立體世界 的來客,其後阿方被顛覆世界觀的故事。
它有幾個不同版本的改編電影 [6] [7] [8] [9]。
臺灣通識網 數學的故事 系列對這本書的導讀
https://www.youtube.com/watch?v=-IbUDqI2Cq4
https://www.youtube.com/playlist?list=PLfS0WrMWEu_47uf3wDOXkVTdycsehWqYI
相關電影
Flatland (1965) - https://www.youtube.com/watch?v=yBbZmwROv84
Flatland (TED) - https://www.youtube.com/watch?v=MGv8MMi8QO0
Flatland (2007) - https://www.youtube.com/watch?v=avMX-Zft7K4
二維平面世界的社會階級
在旅客的印象中,《平面國》的主角 阿方 是一個正方形,是一位律師,在故事開始時已是爺爺輩,有幾個孫子,阿方的回憶與自述構成了整本書的內容。
在阿方所在的二維平面世界,社會的階級地位由其 正多邊形 (regular polygon) 的邊數所決定。
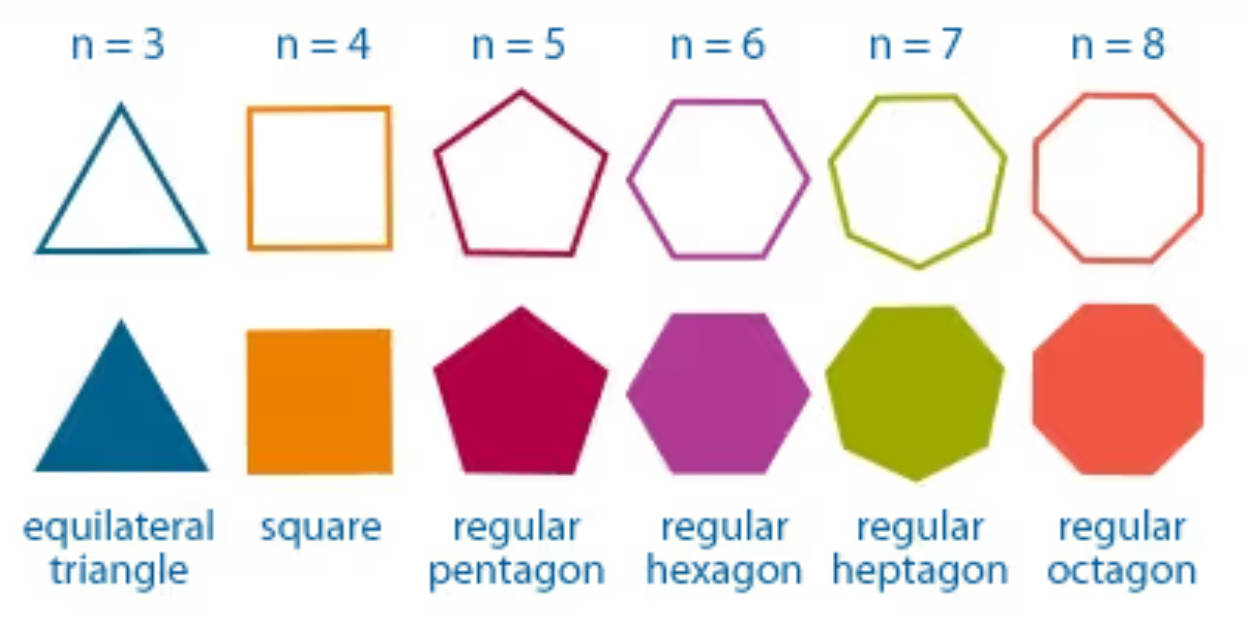
正方形的地位比等邊三角形高,正五邊形比正方形地位高,正六角形比正五邊形地位高,如此類推。
在這個二維平面世界的社會秩序中,平面人們越接近圓形就被視為 "越完美" "越有智慧",也 "越高貴"。像正 100 邊形、正 200 邊形地等 趨近 圓形的人們被視為 接近完美,也是社會秩序中的最高階級 - 祭司。
主角阿方作為正方形,就是在這個社會秩序下的中產階級,
在這個社會秩序中,邊邊相等受到讚美與推崇,而不等邊的多邊形,則被視為次等的,劣根的,甚至是畸形的。

四方︰東南西北
和三維立體世界一樣,二維平面世界有四個方向 - 東南西北。
對於二維平面世界的居民來說,北方 在 "上",南方 在 "下" (二維平面世界沒有上下的概念,這是將三維立體世界的語言翻譯成二維平面世界的語言)。
人們多數生活在五邊形的房子之中,五邊形的住房形狀是法令的要求,五邊形的角 > 90度,沒有那麼尖銳,對行人來說沒有那麼危險。屋頂向北、屋底向南。
下圖是二維平面世界一個房子的 三維俯瞰圖 (二維世界沒有上下維度,無法畫出下圖)。
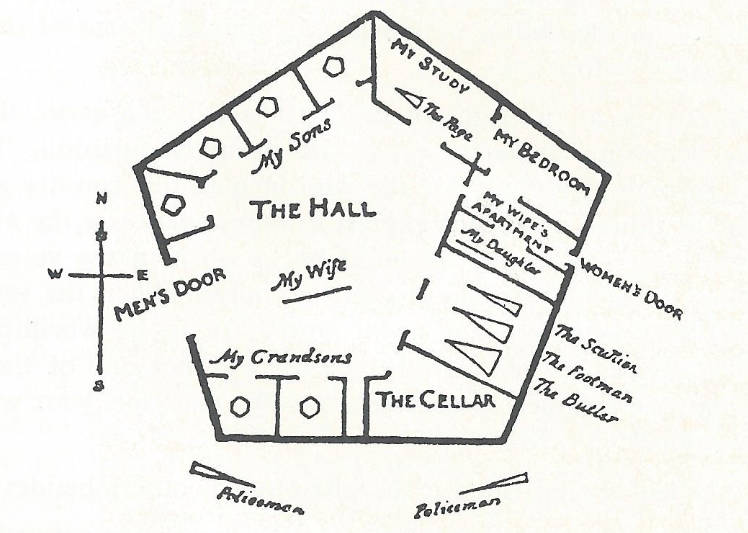
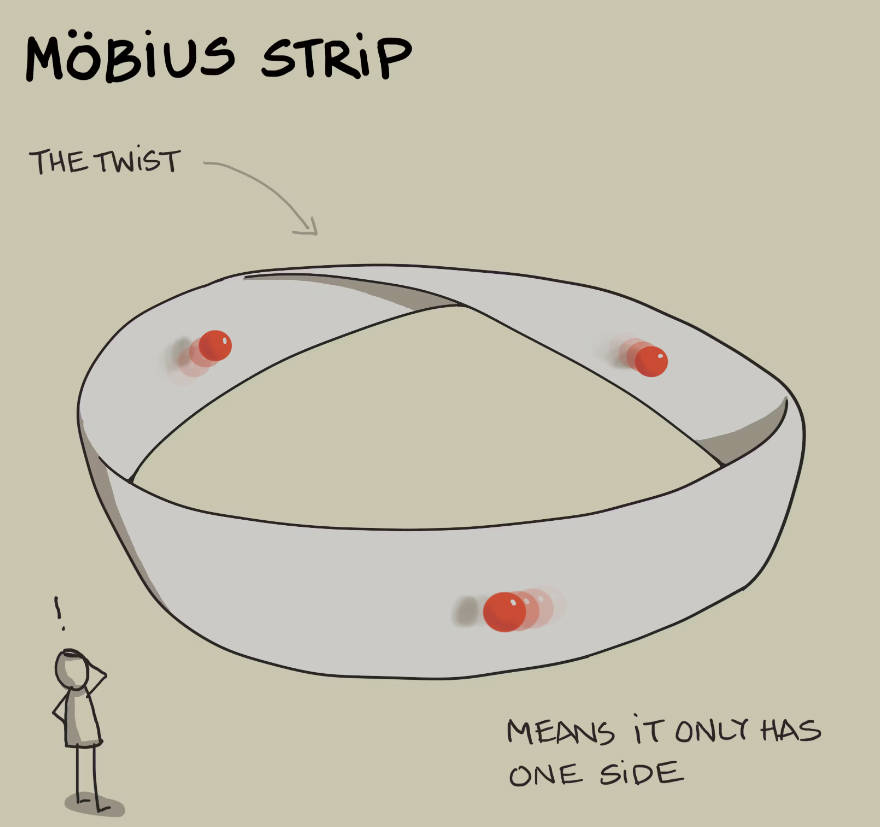
現象世界︰一維、萬物皆線
在阿方的世界,人們眼睛能看到的,其實只有一種幾何 "形狀" - 線。
就像一枚很薄很薄很薄硬幣,上向下俯瞰是一個圓形,而將硬幣 自旋 90 度,就會看到它的 "側面" 接近一條線。

所以阿方每天看到的都是一條線,摸到的是一條線,聽到的聲音也是由線反射而成。
除了線還是線,除此之外沒有其他東西。
在二維平面世界,其感官是一維線性的 (觸覺、視覺、聽覺)。
那二維平面世界的人們,是如何區分不同的 幾何圖形 的呢?
他們主要用三種感官來區分 幾何圖形,耳朵聽覺、皮膚觸覺 和 眼睛視覺。
低等知覺技藝︰耳朵聽覺辯識
在二維平面世界裏,聽覺雖然被使用去辯識不同的 "居民",但比起觸覺與視覺,聽覺難以準確地辯識出一個人的 "幾何圖形"。
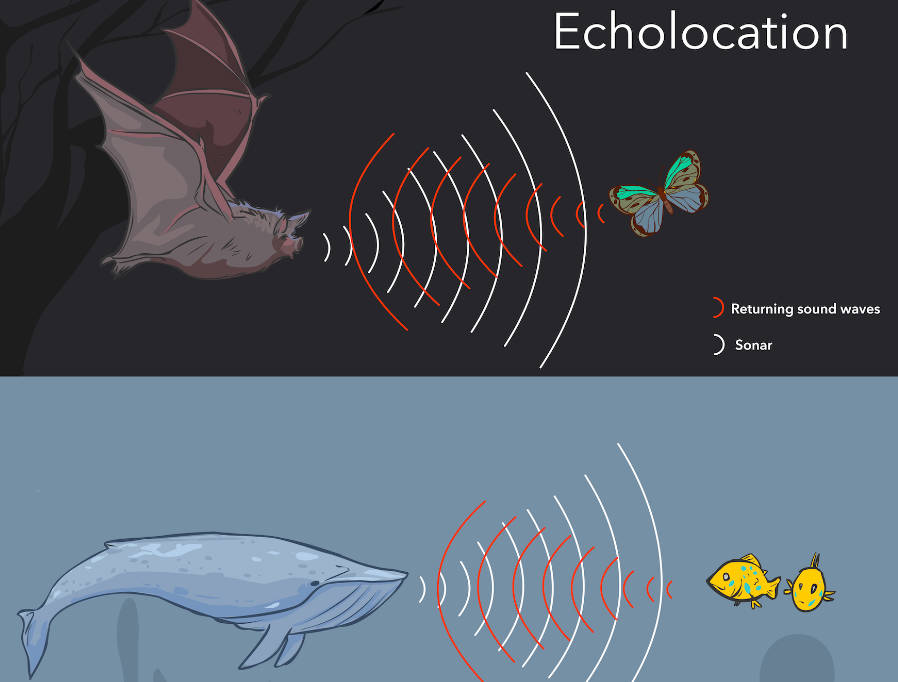
二維平面世界的居民沒有如海豚、鯨魚、蝙蝠等動物一樣的回聲定位 (echolocation) 器官與知覺,這些神奇的動物可以主動發出高頻聲音後利用其回音定位一個物體的距離、位置、形狀。
這個世界的居民也沒有發展足以辯識出物體形狀的雷達科技 -《平面國》在 1884 年出版,那時還沒有雷達與聲納的概念,一些動物能回聲定位也未被人們發現。
如此在阿方所在二維平面世界,聽覺在辯識圖形上遠不如皮膚觸覺 & 眼睛視覺。
低等知覺技藝︰皮膚觸覺辯識
在二維平面世界,觸覺是最簡單地區分圖形的方式,不同的幾何圖形有不同角度,銳角 ( 小於 90 度) 與鈍角 ( 大於 90 度小於 180 度) 的 "觸感" 不同,不同幾何圖形身上的角的數量也不同,三角形 3 個角,正方形 4 個角等等。
儘管皮膚觸覺是如此的 "直觀",但平維平面世界的居民仍然需要在學校學習去使用觸覺去補全 知覺 (perception)。角的大小,銳角鈍角,它們能構成甚麼幾何圖形等等並不單單靠 "摸" 就能 "摸出來","摸" 只是構築 知覺 (perception) 的一部份。
有經驗的盲人摸一點點就能在知覺中構築出他摸到的是甚麼,沒有太多經驗的盲人需要摸得更多摸得更長時間,才知道他接觸的是甚麼。
在二維平面世界,皮膚觸覺被視為一種低等的構築知覺方法,通常在沒有受到太過教育的中下階層使用,社會更高的階層後代需要學習打磨的則是另一種知覺技藝 - 眼睛視覺。

高等知覺技藝︰眼睛視覺辯識、霧、明暗、深度
在二維平面世界的中上層社會裏,靠著觸覺來辯識他人的幾何形狀是被視為 "原始" "不禮貌" 的,
依靠 "視覺" 來辯識幾何圖形被視為高雅且得體。如此,中上階層將他們的子弟送入教授視覺辯識高等技藝的學校,來磨練他們後代的眼睛。
問題在於,在二線平面世界的角度,所有人看到的都是 "一條線",那麼他們到底如何區分 "由三角形投影出的一條線" 還是 "由正方形投影出的一條線"?竟然任何幾何圖形在二維平面世界投影的都是 "一條線","區分辯識" 到底如何可能?
關鍵在於二維平面世界普遍存在的 "霧",有 "霧" 的存在,"遠" 的東西會比 "近" 的東西看起來模糊,"角" 會比 "邊" 看起來更「明亮」 (Φοίβη = Phoebe = 明亮),有「明亮」就有「暗影」 (Έρεβος = Erebus = 暗影)。
因為 "霧" 的存在,不同幾何圖形在二維平面世界所投射的 "線",在視覺上是有區別的,它們的 "深度" 不同,透過 "霧" 折射到眼睛形成的影像有區別。
而二維平面世界的高等學校,學習的就是透過這種明與暗產生的 "區別",來構築視覺知覺。通過一維線段的 "投影",去透過 心智 (νούς = nous = intellect = 心智 = 神智) 來 "還原" 一個二維的幾何圖形。



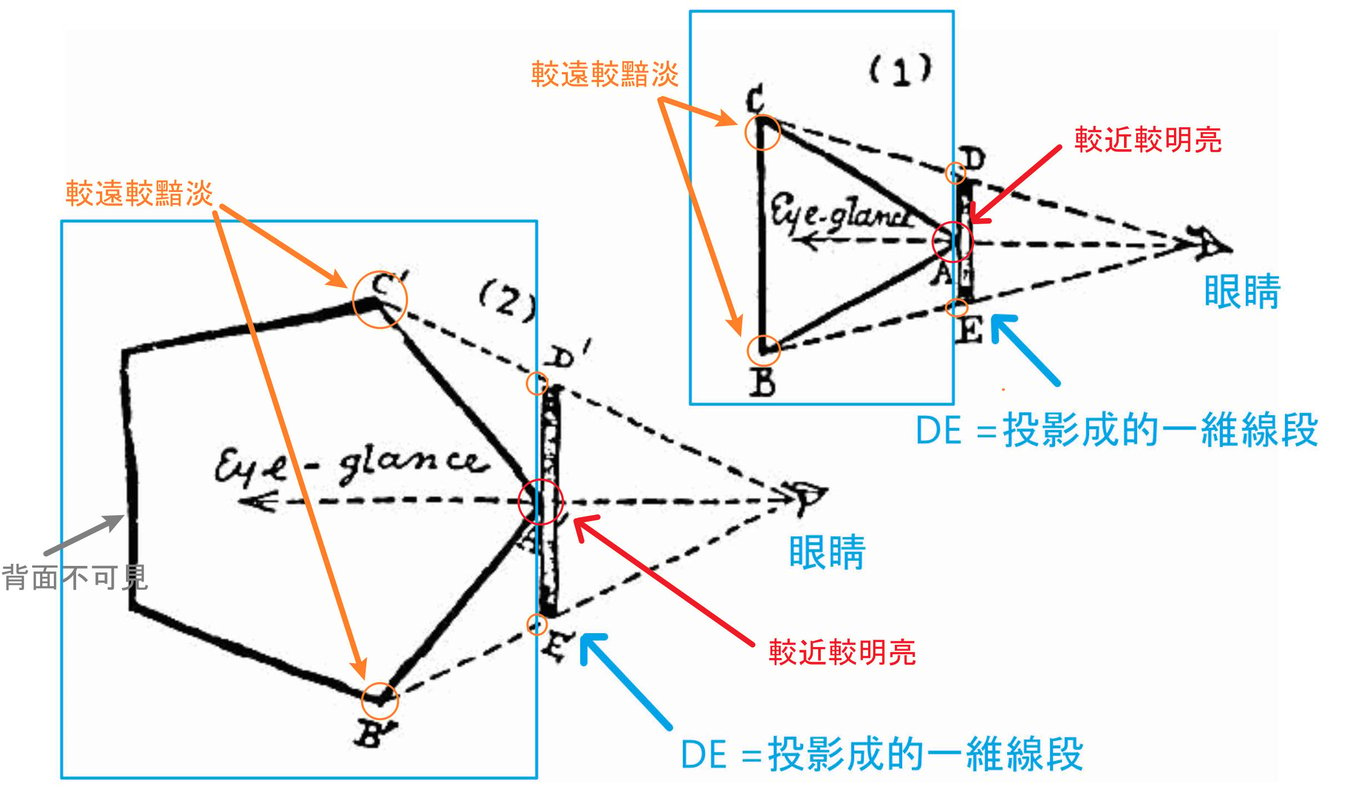
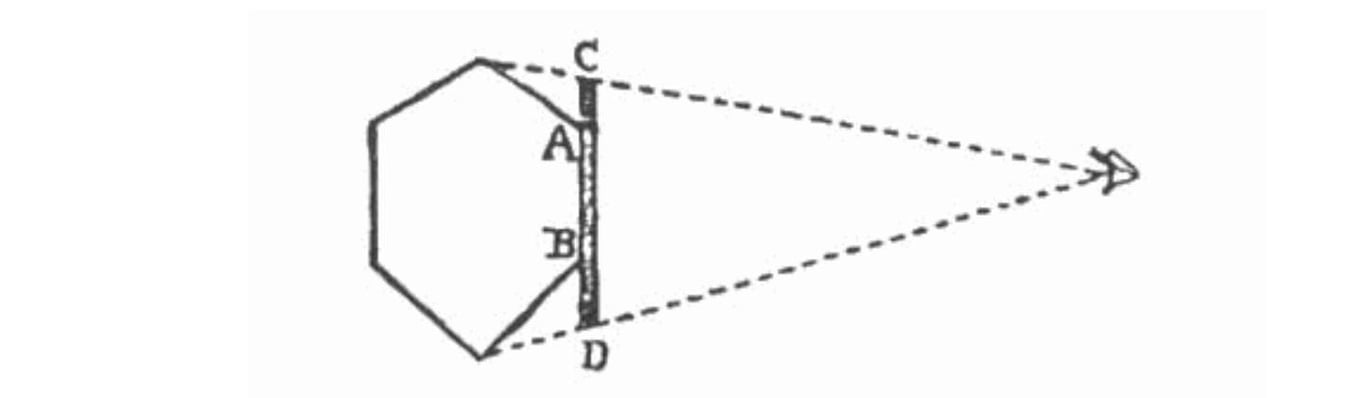
下圖是《平面國》中阿方解釋在他們的社會,如何靠視覺辯識出一個幾何形狀。
圖中 "眼睛" 在右,虛線是光線的路徑,DE = 投影成的一維線段 (與眼睛成像成比例)。
因為霧的普遍存在,幾何圖形中離眼睛較近的 "角",會顯示得較為 "明亮",而離眼睛較遠的 "角",會顯示得較為 "黯淡"。
三維立體世界的人類視覺
類同 (αναλογία = ανά + λόγος = analogy = 比喻 = 類同) 於二維平面世界的視覺知覺轉化,三維立體世界的人們 (我們) 所 "看到" 的,其實也是一個三維物體的二維投影。
我們看一張被繪畫在紙上的畫,我們感官 (sense) 上看到的是一張 "二維的紙",但知覺上 (perception) 感知 (perceive) 到的卻是立體的畫面,這個被感知的 "深度" 是從何而來?



人們能在畫中 "感知" 到 "深度",這和畫家使用了不同的繪畫技法有關 [12],這些技法包括
使用 "霧" 讓近的清晰,遠的模糊,近的更多紋理,遠的更少紋理
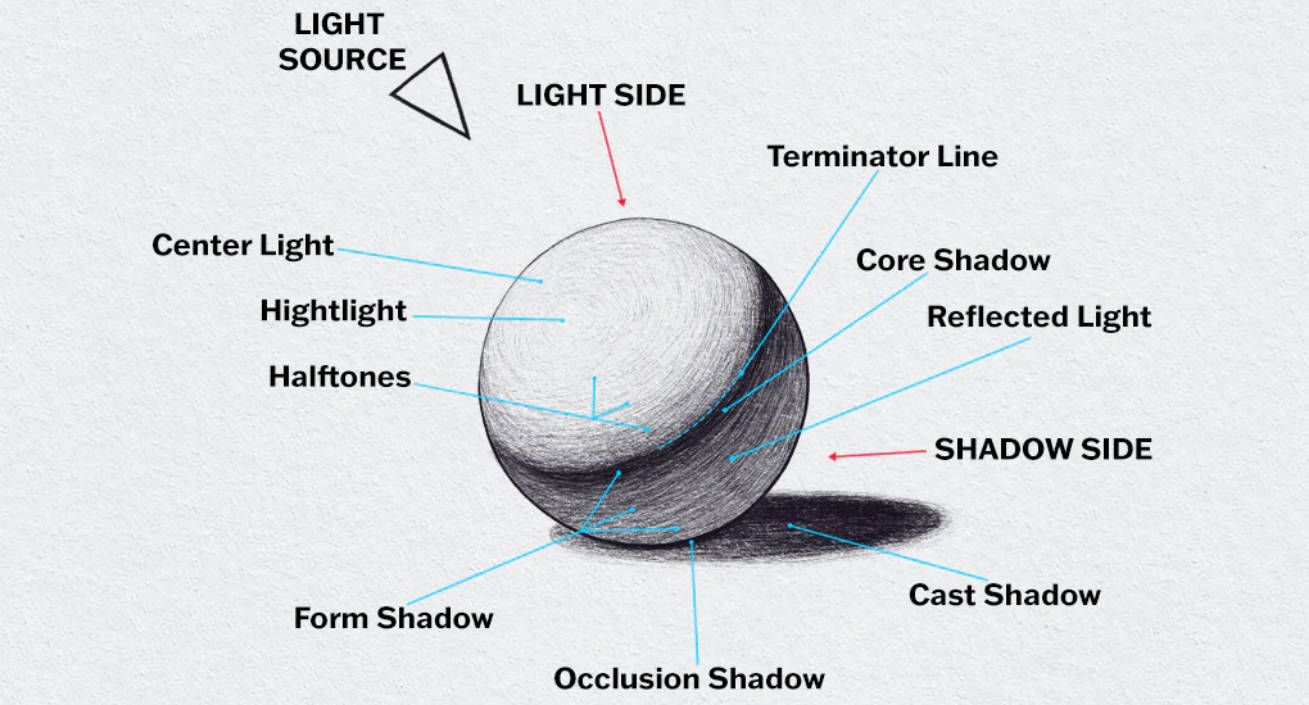
光與影的差別,在物體表面產生出層次立體感
物體的重疊,在前的可見,在後的被部份遮蔽
等等
透視法 & 射影幾何
文藝復興時期開始,畫家有意識地組織幾何線條,用透視法的構圖來讓他們的作品更加的 "趨近" "真實",更能映照出 "可見的秩序" [14] [15]。
使用透視法的《最後的晚餐》,作者︰達芬奇 (Leonardo da Vinci)。

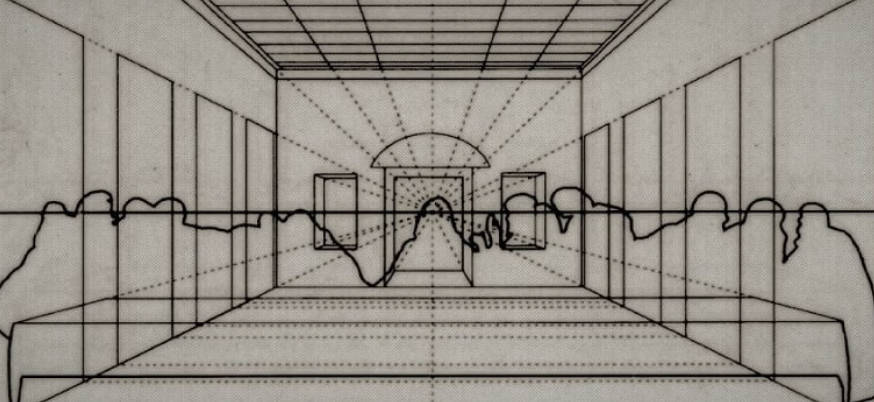
《雅典學派》(Scuola di Atene),作者 拉斐爾 (Raphael)。


畫家為了精準 "還原" 他們可見的幾何秩序,還製造出輔助繪畫的機器 [16]。

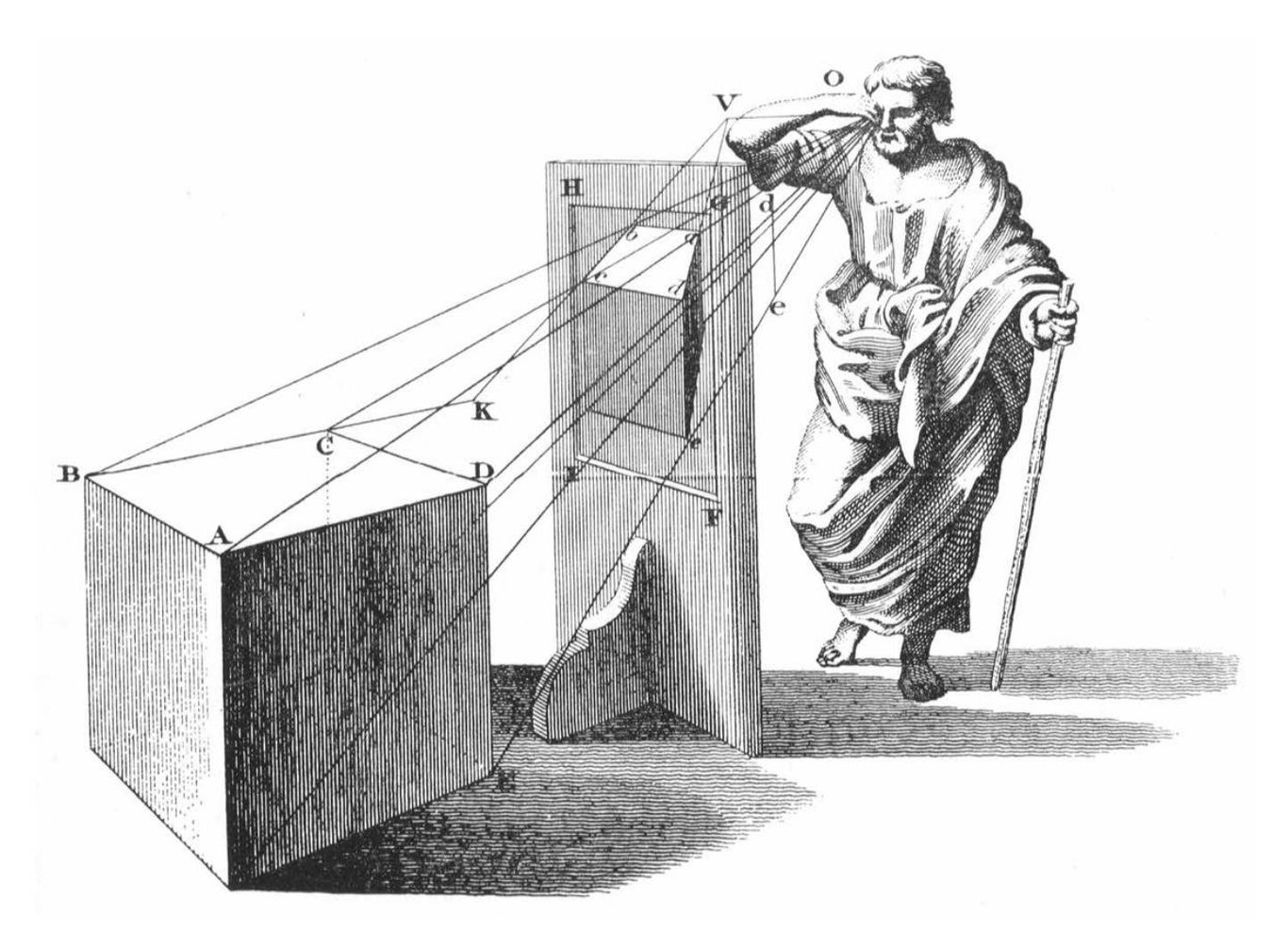

若果我們處於地面的正上方,像衛星一樣看著正下方的地面,平行線不會相交。

我們回到地面,會發現在我們地面的視角裏,公路所形成的平行線,似乎在視覺上在超遠處 "相交" 了,這個地面視角下平行線在超遠處 "相交" 的 "點",被畫家稱為消失點 (vanishing point) [17]。
在地面視角下,平行線在 無限遠處 "相交"。

透視技法相關的數學是 射影幾何 (projective geometry) [17]。

日常的感覺、知覺、意識
三維立體世界的我們,只要睜開眼睛,就會一直接收眼睛所 "看到" 的二維平面畫面,而雖然眼睛接收到的畫面是二維的,但人體的構造與後天的習慣,讓我們能 "自動而無意識" 地將這些不間斷的二維平面畫面轉化為三維立體的知覺。
就在此時此刻,當我們看著電話手機或電腦時,我們會覺得自己是身處於一個三維立體的空間,所有的 "運動" "改變" "時間差異" 都是在這個三維立體空間進行,然而我們感官上一直看到的只是一個二維的畫面。
我們一直在使用 "看到" 的二維平面,去 "演化" "推斷 (infer)" "猜測" "感知" 一個我們認為是 "日常" 的三維空間。
類同 (αναλογία = analogy) 於《平面國》的居民,阿方的眼睛只能接收到 "一條線",是他透過經驗與學習,無時無刻地將 "一條線" 推斷 (infer) 為 "一個二維圖形"。
畫家透過模仿這種可見的視覺幾何秩序,某程度上是在進行一種精巧的魔術,用繪畫的技藝去讓人們相信自己在一張紙的平面上看到了三維的空間。
錯覺的可能
光學錯覺 (optical illusion) 則有意的利用人們的知覺傾向,去製造迷惑 [18]。









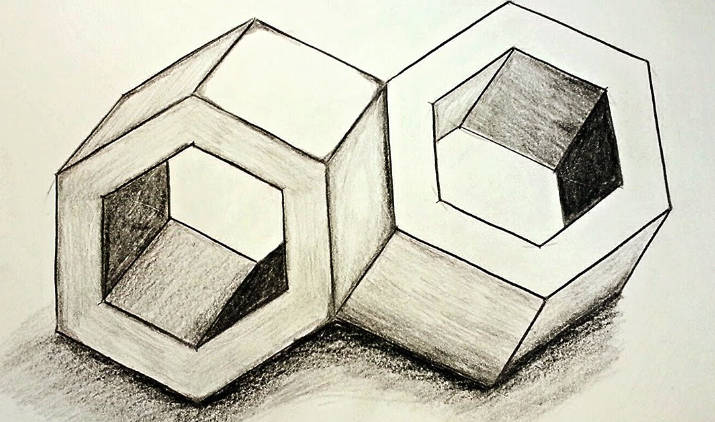



投影作為錯覺
這些光學錯覺讓我們不自覺地從感覺推斷 (infer) 到知覺的意識,讓我們以為接收到的二維平面已足夠還原出三維立體,讓我們相信僅靠一個二維畫面會讓我們知道 "真相"。
二維畫面可以透過不同的手段 "模仿",而讓人產生感知到了有一個三維立體在面前;一幅巨大的畫在近距離觀看,會令人們覺得這是真實的景象;只要投影的細節足夠令觀看者信服,人們就假定投影背後是他們熟悉的存在。
錯覺 (illusion) 在於我們感覺 (sense) 接收到的畫面當然 "存在",那個錯覺的畫面是 "真實的投影" ,然而我們從 感覺確定性 (sense-certainty = sinnliche gewissheit) 推斷 (infer) 到 知覺 (perception) 的過程出了偏差。
而這也不能怪 感覺確定性 (sense-certainty),因為我們的眼睛只能接收二維的畫面,感覺確定性 (sense-certainty) 一直就是如此的運作,只能接收到全景的 "一部份"、"一個切面"、"一個投影"。
或者我們眼前的手機或電腦只是一張紙?
就在此時不只視覺知覺陷入了錯覺,連觸覺知覺也陷入了錯覺讓我們相信摸到的不是一張紙而是手機,耳朵其實一直戴著耳機但忘了放下來,所以聽到的遠近都是偉大錯覺的完美同步,而這些感官顯現的刺激全都是真的,只是我們在無意識 推斷 (infer) 的過程中出了嚴格的偏差,把片段的 "射影 (projection)" 當成了完整的 "源頭",是射影幾何 (projective geometry) 作品的一部份。
而某一天某一個乘著直升機飛行的人,飛到我們的正上方,看到地面的我們把一張紙當成手機不斷的操作,他也陷入了「這個在地面的人在做甚麼」的巨大迷惑之中。
希望 (Ελπίς = Hope) 部份或者在於 錯覺 (illusion) 為不完整的投影。
投影源頭的運動、旋轉,總會產生一些幽微的線索,若果陷入錯覺的人們閉上眼睛,不將 100% 的注意力執著於投影的表象,而在回憶中尋找異常的痕跡,細心的計算慣性外的非凡,也許能尋覓到出口的一線光亮,聽到正上方直升機產生巨大轟鳴而往上望,那是可能性的直角 (ορθή γωνία = right angle = 正確的角度)。

二維投影下的知識高塔
陌生旅客發散的走神從錯覺再次回到《平面國》故事中對祭司教士階層的描述。
在二維平面世界,趨近圓形的多多多邊形是其社會秩序的最高階層,故事中的主角阿方解釋
當我稱他們為祭司時,請不要誤解我只是指你們所理解的詞義。對我們來說,我們的祭司是所有業務、藝術和科學的管理者;貿易、商業、將領、建築、工程、教育、政治、立法、道德、神學的指導者;他們自己不做任何事情,卻是他人所做的一切有價值的事情的原因。
這些趨近圓形的祭司,是整個社會的哲學家、神學家、形而上學家以及核心統治者,他們是擁有最多 "知識" 的貴族,他們立法、釋法,並 "學習與維護" 他們知覺之中的 自然法 (natural law)。
儘管社會上稱這些祭司為「圓」,但所有人都知道,沒有一個「圓」真的是「圓」,所有的「圓」都只是多多多邊形的趨近 ( 300 邊形、400 邊形、500 邊形如此類推)。
二維投影下的教義
而祭司們對形而上學 (metaphysics)、自然法 (natural law) 的理解,就會轉化及普及成一般民眾的教義、律法、文化、習俗、一切潛移默化的所思所想所行所做。
而阿方所在的平面社會秩序,其核心教義則為
至於「圓」的教義,可以簡單地概括為一句格言:「關注你的幾何形態 (Attend to your Configuration)。」無論是政治、教會還是道德,他們所有的教導都以改善個人和集體的幾何形態為目標,當然特別關注圓圈的形態,其他一切都是次要的。
也就是說,阿方所在社會,以成為幾何圖形上的「圓」為最高價值,越多邊的正多邊形是對「圓」的模仿,因而 12 邊比 10 邊高貴,10 邊比 5 邊高貴。而 3 邊的三角形則構成了社會基層,3 邊的三角形再分為與圓 "更相似" 的等邊三角形,次一級的等腰三角形,除此之外的三角形是更劣等的存在。

「以圓為本、關注形態」就是阿方所在秩序的核心價值觀 & 核心世界觀,是的整個社會序列的基础。
二維平面世界曾經有一名著名的哲學家,他的名字是 Pantocyclus (panto + cyclus = 處處皆圓),這位哲學家的形而上學可以總結為
所有的過失或缺陷,從輕微的不當行為到最嚴重的罪行,Pantocyclus 都歸因於身體幾何形態的某種偏差,可能是由於人群中的某些碰撞引起的(如果不是先天性的),由於忽視鍛煉或過度鍛煉,甚至由於溫度的突然變化,導致身體某些過於敏感的部位收縮或擴張。因此,這位傑出的哲學家得出結論,無論是良好的行為還是不良的行為,在任何清醒的評估中都不是值得稱贊或責備的合適主題。例如,為什麼你應該贊揚一個正方形的誠實,他忠實地捍衛客戶的利益,而實際上你應該更加欽佩他的精確的直角呢?或者,為什麼你應該責備一個說謊、偷竊的等腰三角形,而實際上你應該哀嘆他的兩邊不可治愈的不平等呢?
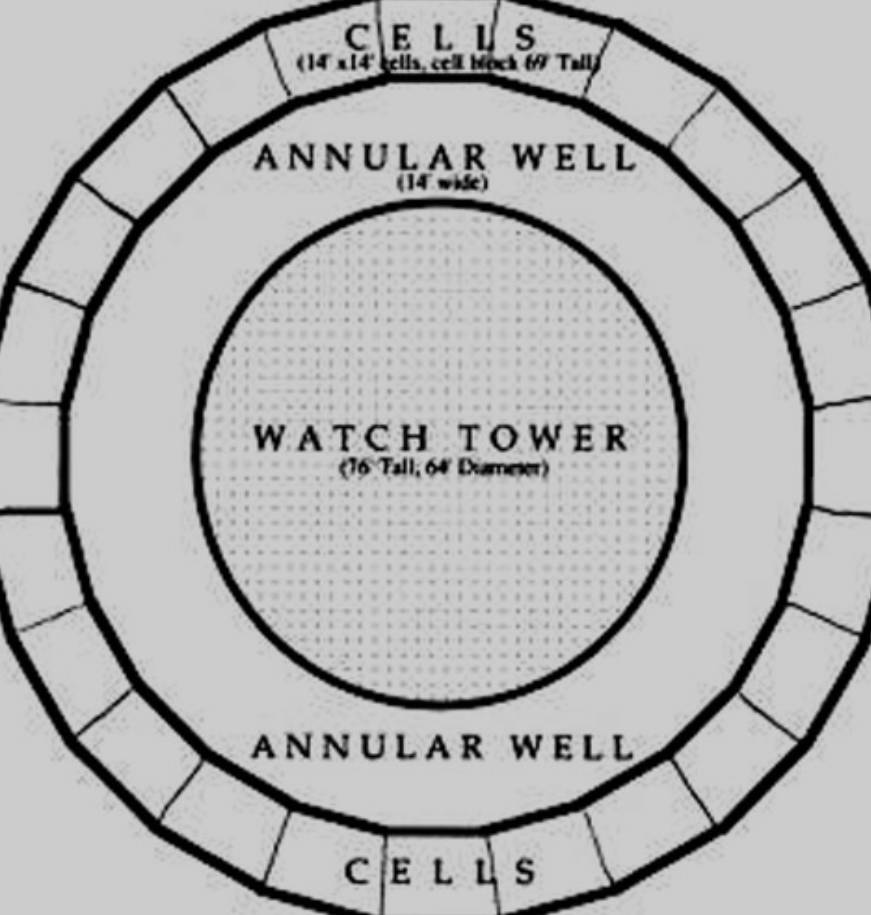
整個社會最關心的,是形態上「趨近於圓」,一切的價值的砝碼都加權在幾何圖形上,沒有太多價值放在看不見的德性 (ἀρετή) 諸如 節制 (σωφροσύνη)、勇氣 (ἀνδρεία)、正義 (δικαιοσύνη)、智慧 (σοφία) 等等上,阿方所在的社會只能感知到「趨近於圓」的高貴 & 美 (καλός)。
阿方所在的社會按著這種秩序,自時間開始以來,已運行了兩個千禧年 (《平面國》的情節圍繞著 1999 年過去, 新的千禧年 2000 要到來展開)。
當然,這個「關注形態,以圓為本」的教義,也會時不時遇上現實釋義的困難
從理論上來說,這個原則是毫無疑問的;但它也存在實際上的缺點。當面對一個等腰三角形時,如果一個無賴辯稱他因為不平均而無法停止偷竊,你可以回答說,正因為他無法不給鄰居帶來困擾,你作為法官就無法不判他被物理消滅,這就是問題的結束。但在一些小的家庭糾紛中,消滅或死亡的處罰是不合適的,這種形狀的理論有時會變得尷尬;我必須承認,有時當我的六邊形孫子以溫度的突然變化為他不服從的藉口時,他認為我應該將責任歸咎於他的形狀,而不是他自己,而他的形狀只能通過大量的最好的糖果來加強,我既無法從邏輯上拒絕他的結論,也無法在實際上接受他的結論。
阿方也觀察到,他所在社會的高層,並不完全按著最僵硬的教義來教孩子
就我個人而言,我覺得最好假設一番好好的責罵或訓斥對我孫子的形態有一些潛在的增強影響;盡管我承認我沒有任何理由這樣認為。無論如何,我在擺脫這個困境的方式上並不孤單;因為我發現許多最高層的圓圈,在法庭上擔任法官時,對於規則和不規則的圖形使用表揚和責備;而且我通過經驗知道,在他們的家庭中,當他們責罵他們的孩子時,他們會像熱情洋溢地相信這些名字 (對與錯) 代表真實存在一樣,激烈地談論「對」或「錯」,以及一個人類的圖形真的能夠在它們之間做出選擇。
在阿方的社會,300 年前,祭司統治者認為女性的理性不足,所以停止讓女性接受教育。
大約 300 年前,由於女性在理性方面的不足,但情感方面豐富,"首席主圓" 決定不再將她們視為理性的存在,也不再給予她們任何心智教育。結果是,她們不再被教導閱讀,甚至連掌握算術的能力都不足以讓她們計算丈夫或子女的角度;因此,她們在每一代中的智力能力明顯下降。而這種女性非教育或靜心主義的制度至今仍然存在。
而阿方憂心這會讓社會整體沉淪,比起 300 年,當代二維世界的居民智力上在漸漸下降。阿方認為高層有必要讓女性重新接受教育。
我已經能夠感覺到,與三百年前我們祖先更強大的智力相比,現在對數學真理的理解力已經出現了一些薄弱之處。我不提及一個女性如果偷偷學會閱讀並將她閱讀一本流行書籍的結果傳達給她的同性朋友可能帶來的危險,也不提及一個嬰兒男性的不慎或不服從可能向母親透露邏輯辯證的秘密。基於男性智力的衰弱,我謙卑地呼籲最高當局重新考慮女性教育的規定。
阿方的觀點仍被自己多年的世界觀慣性所局限。
二維秩序的有力反對者
圓形祭司階層所定的「關注形態,以圓為本」秩序,在二維世界的歷史中,曾經受到過有力的挑戰者。
在歷史上,人們發現,幾何形態的辯識,其實可以透過將不同的邊塗上顏色來區別,

年復一年,士兵和工匠們開始更加激烈地主張,並且越來越真實地認為,他們與最高階層的多邊形之間並沒有太大的區別,現在他們與後者平等地提升了地位,並且通過簡單的顏色識別過程能夠應對生活中的所有困難和問題,無論是靜態的還是動態的。他們不滿足於視覺識別逐漸被忽視的現狀,大膽地要求法律禁止一切“壟斷和貴族化的藝術”,並隨之廢除所有用於視覺識別、數學和感知研究的資助。不久之後,他們開始堅持認為,由於顏色作為第二自然已經摧毀了貴族化的區別的必要性,法律應該順應這一趨勢,從此將所有個體和所有階層都視為絕對平等並享有平等權利。
「顏色主義者 (Chromatistes)」對「形態主義秩序」發出了有力的挑戰。
「顏色主義者」提出了一個新的形而上學與價值觀 - 「顏色解決一切,七彩等於美滿」。
然而,「顏色主義價值觀」的實行,卻有了意料之外的副作用。
科學、藝術被視為多餘,社會整體的智性在下降。
視覺辨識的藝術已不再需要,因此也不再被實踐;幾何學、靜力學、動力學和其他相關學科的研究很快被視為多餘,甚至在我們的大學中也受到了輕視和忽視。在我們的小學中,感覺的次級藝術也很快遭遇了同樣的命運。

它也造成了意料之外的混淆 - 混淆圓形與線條。
請記住,在顏色革命時期,視覺識別的衰退對社會構成了威脅;再加上女性很快會學會淡化自己的四肢以模仿圓形,那麼,親愛的讀者,對你來說,顏色法案使我們面臨將牧師與年輕女性混淆的巨大危險顯然是明顯的。
「顏色主義」的初衷是削弱貴族階級,卻無意中讓原來的貴族階級更強 (因為保留了智性)。
該法案的第二個目標是逐漸削弱圓形社會的道德觀。在智力的普遍衰退中,他們仍然保持著他們原始的清晰和理解力。從幼年時起,他們在圓形家庭中習慣了完全沒有顏色的環境,只有貴族們保留了神聖的視覺識別藝術,並從那種出色的智力訓練中獲得了種種優勢。因此,在普遍顏色法案出台之前,圓形社會不僅保持了自己的地位,甚至通過避免流行時尚而擴大了與其他階級的差距。

「顏色能解決一切」的思潮下,人們還發現「利用顏色」來進行欺騙,因為在新制度下,人們只相信顏色。
碰巧,一個智商幾乎不到四度的低等腰三角形,無意中涉足了一些他所掠奪的商人的顏料,他自己或者是讓別人幫他塗上了十二邊形的十二種顏色(故事版本不一)。他走進市場,用一個假聲攀談了一位孤兒少女,她是一位貴族多邊形的女兒,他在過去曾經徒勞地追求過她的愛情;通過一系列的欺騙手段——一方面是一連串太長無法細數的幸運事件的幫助,另一方面是新娘的親屬幾乎難以置信的愚蠢和對常規預防措施的忽視——他成功地完成了這場婚姻。這位不幸的女孩在發現自己受到的欺騙後自殺了。
「顏色主義」VS「形態主義」的鬥爭,最後以一場血腥的政變與內戰結束,智性上佔優的舊祭司,利用手段清除了「顏色主義者」。

在那之後,顏色在全國被禁用。
阿方聽說,顏色只會在一些最高級與最深奧的課程中出現。
不用說,從此以後,使用顏色被廢除,擁有顏色也被禁止。除了由圓圈或合格的科學教師使用,任何表示顏色的詞語的發聲都會受到嚴厲的懲罰。只有在我們的大學裡,在一些最高級和最深奧的課程中——我自己從未有幸參加過——據說仍然允許適度使用顏色來說明一些更深層次的數學問題。但這只是我聽說的。
顏色的秘密以一種殘忍的方式在最高層傳承。
在平面世界的其他地方,顏色已經不存在了。製造顏色的技術只有一個人知道,那就是現任的首席圓形人;他在臨終前只會將這項技術傳給他的繼任者。只有一家工廠生產顏色;為了防止秘密外泄,工人們每年都會被殺掉,然後再引進新的工人。即使到現在,我們的貴族階級對於遠古時期普遍顏色法案的騷動仍然感到恐懼。

黃昏的貓頭鷹
對於三維立體世界俯瞰這一切的人們來說,無論「形態主義」還是「顏色主義」都有巨大的缺陷,但身處二維平面世界的居民,他們意識到的可能性非常有限,他們只會造作他們視野中可見的選擇。
儘管「以形為本」還是「以色為本」的哲學都顯得不完備且注定趨向災難,然而他們雙方都彼此真心認為自己擁護的哲學能解決一切。他們雙方無法意識到,無論是「形」還是「色」都是三維立體世界對二維平面世界的投影。三維立體世界的人們知道,有更深一層的東西存在,單純的追求「形」還是「色」都無法解決二維世界的無知、問題、沖突。
三維立體世界的人們奇怪為何二維人們為如此不完備的哲學戰鬥而死,二維平面世界的人們則對三維居民的空想感到不可思議,視之為不是純粹的幻想就是魔鬼的呢喃。

阿方造訪一維線性世界
在公元 1999年的倒數第二天,《平面國》的主角阿方做了一個夢。
在夢中,作為二維正方形的阿方,在不知名的空間中,看到一個 "線空間",在這個 "線空間" 上,阿方看到了不同的線段。
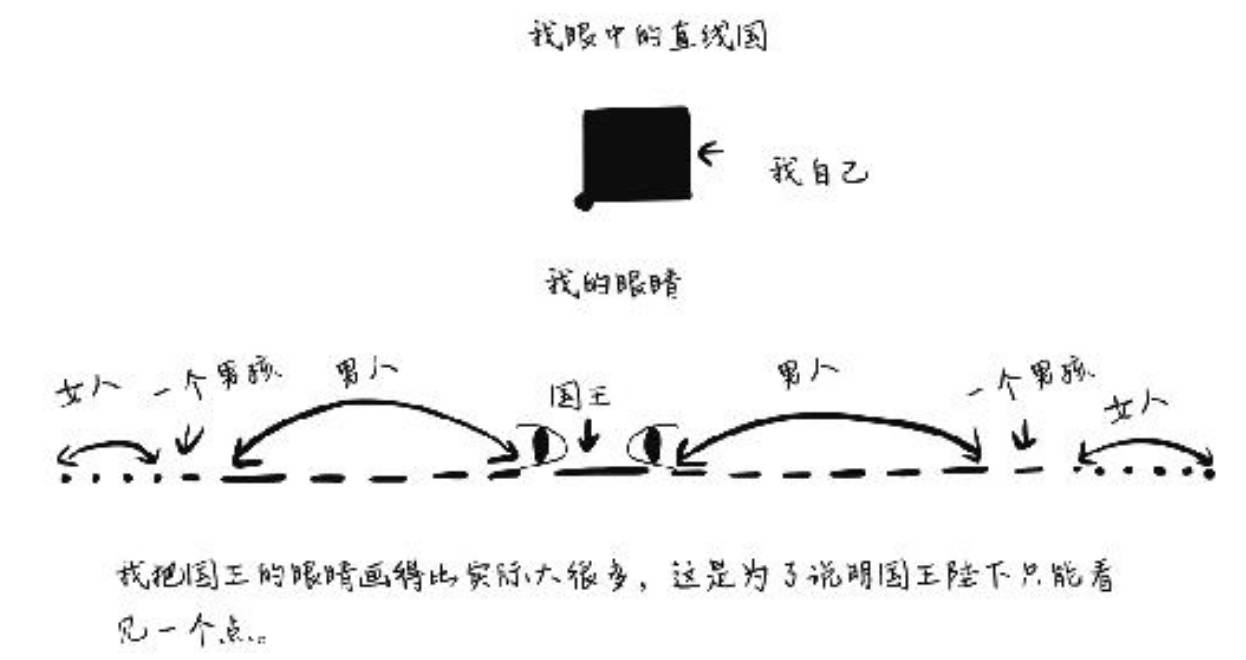
在這個一維線性世界,最長的 "線" 就是國王,在這個一維國度,長度就是最高價值,是秩序之基础。
起初阿方嘗試和 "線國國王" 對話,但發現 "線國國王" 不知道阿方的聲音從何而來,阿方的聲音對國王來說,來自一個未知的方向 (因為國王在線空間內,線空間外的事情皆為未知)。
雖然在我第一次對他說話時,他聽到了我的聲音,但這種聲音對他來說完全超出了他的經驗,所以他沒有回答,他說他"看不見任何人",只聽到一種聲音,就像是從他的內臟中傳來的。
在國王的角度,阿方的聲音像是 "從內部傳出"。
對於一條線來說,左端和右端是 「側」,而左端和右端之間皆為 「內」 (εσωτερικός = esoteric = 內),而既非 「側」 亦非 「內」的,是 "外" (εξωτερικός = exoteric = 外)。
國王以為他所 "感知" 的 "線空間",就是世界的全部。
這個可憐無知的君主,自稱為他的國度,也就是他存在的那條直線,他相信這就是整個世界,甚至整個空間。他既不能移動也不能看見,除了在他的直線上,他對於其他事物毫無概念。
這些聲音在我所稱的他的側面,但他稱之為他的 內部 (εσωτερικός = esoteric = 內) 或胃部,不斷撞擊著。他對我來自的地方甚至現在也沒有絲毫概念。在他的世界或直線之外,對他來說一片空白;不,甚至不是空白,因為空白意味著空間;可以說,一切都不存在。
在這個一維的線性國度,聽覺是最重要的分辨知覺 - 因為所有人都只能看到一個點,類同於平面世界的居民的感知只是一條線,三維世界的居民所看到的是一個二維平面。
不用說,他們的視野只有一個點;除了點,沒有人能看到其他東西。男人、女人、孩子、物品——在線條人的眼中,每個人都是一個點。只有聲音才能區分性別和年齡。
在阿方的眼中,一維世界是相當的沈悶、單調、枯燥無味;但他意外的發現國王非常有活力。
這樣的生活,所有的視野都限制在一個點上,所有的運動都限制在一條直線上,對我來說無比沉悶;而國王的活力和快樂讓我感到驚訝。
阿方嘗試向一維國王解釋,在這個世界,除了有北方與南方外,還有東方與西方 (左與右),而一維國王則表示不解,然後兩人進行一輪溝通失敗的對話。
國王︰...讓我問一下你所謂的 '左' 和 '右' 是什麼意思。我猜想這是你的方式來表示北方和南方
阿方:不是這樣的,除了你所說的南北運動,還有另一種我稱之為從右到左的運動。
國王:如果可以的話,向我展示這個從左到右的動作。
阿方︰不行,除非你能完全走出你的線。
國王:你說我不屬於我的領地?你是指我不屬於這個世界?不屬於空間?
阿方︰嗯,是的。超出了你的世界。超出了你的空間。因為你的空間並非真正的空間。真正的空間是一個平面;而你的空間只是一條線。
國王:如果你無法自己在左右移動中指示這個動作,那麼請你用言語向我描述它。
阿方︰如果你分不清左右,我恐怕我所說的話無法讓你明白我的意思。但是你肯定不會對這麼簡單的區別一無所知。
國王:我完全不明白你的意思。
阿方︰唉!我該如何解釋清楚呢?當你直線前進時,有沒有想過你可以以其他方式移動,轉動眼睛朝向你現在正面的方向?換句話說,除了總是朝著你的極端部位移動,你從來沒有想過想朝著你的側面 (εσωτερικός = esoteric = 內) 移動嗎?
國王:絕不可能。你是什麼意思?一個人的內部 (εσωτερικός = esoteric = 內) 怎麼可能有「前面」?或者一個人怎麼可能向 內部 (εσωτερικός = esoteric = 內) 的方向移動?
當發現語言完全無力,彼此的語言系統存在著不重疊的區域時,阿方打算用行動與結實的 "現象" 去說服國王 - 阿方打算將自己 "投射" 到一維空間,讓國王 "感知" 到他的真實存在。
阿方成功的讓國王 "感知" 到他的 "投射"。
在我開始移動身體離開線國的那一刻,只要我身上的任何一部分仍然在他的統治範圍內並在他的視線中,國王就不斷地驚呼著:"我看到你了,我仍然看到你;你沒有移動。"
但是當我最終將自己移出他的線國時,他用最尖銳的聲音尖叫著:"她消失了;她已經死了。"

阿方對線空間進行了一次 "穿越",將整個正方形往線性空間上都過了一遍。
而這個舉動在國王的感知中,就是阿方 "突然" 出現,又 "突然" 消失,像是來了又死了一樣。
"我沒有死," 我回答道; "我只是離開了線國,也就是你所稱之為空間的直線,進入了真正的空間,在那裡我可以看到事物的真相。此刻,我可以看到你的線,或者說你所謂的邊緣或內部;我還可以看到你北方和南方的男人和女人,現在我將逐一列舉他們,描述他們的次序、大小和彼此之間的間隔。"
阿方以為自己實現了 "奇蹟",就能讓國王相信,沒想到國王的世界觀慣性是如此的厚重,國王只是把阿方視為妖邪。

國王的 "線性理性 (linear rationality)" 讓他得出一個 "清晰" 的結論︰阿方並沒有移動,而只是施展了一些魔法般的消失和再現的技巧;阿方所宣稱的 "新世界" 是不存在的。
然後阿方就怒了。
對於他的邪惡行為感到憤怒,尤其對他聲稱對我的性別一無所知感到憤慨,我毫不客氣地回答道:"愚蠢的傢伙!你自以為是存在的完美,但實際上你是最不完美和愚蠢的。你聲稱能看見,但你只能看見一個點!你自誇能推斷出直線的存在;但我能看見直線,並推斷出角度、三角形、正方形、五邊形、六邊形,甚至圓形。何必再浪費言語呢?足以說明,我是你不完整自我的完整體。你是一條線,而我是線中之線,萬線之線,我國稱之為正方形:即使我比你優越得多,但在平面國的偉大貴族中,我也微不足道。我來訪你,是希望能為你的無知帶來光明。"
阿方的傲慢,成功地激怒了一維國王,並嘗試攻擊阿方。
聽到這些話,國王向我走來,發出威脅的吼聲,彷彿要把我從對角線上刺穿
然後阿方的夢就醒了。
來自三維立體空間的訪客
在阿方 "夢" 到訪問一線世界的後一天,阿方遇到了來自三維立體空間的訪客。
這是我們時代的1999年的最後一天。雨滴的聲音早已宣告了夜幕降臨;我坐在妻子身旁,沉思著過去的事件和未來一年、一個世紀、一個千禧年的前景。
在阿方居住的房子,出現了一個陌生的聲音,還出現一個 "人",這令阿方和他的妻子十分驚恐。
我和我的妻子都聽到了那些話,盡管她不明白它們的意思,但我們倆都朝著聲音的方向跳了過去。當我們看到眼前的一個身影時,我們感到了恐懼!乍一看,它似乎是一個側面看到的女人;但經過一會兒的觀察,我發現它的四肢過於迅速地變得模糊,無法代表女性;我本以為它是一個圓,只是它似乎以一種對於圓或任何我曾經經歷過的規則圖形來說是不可能的方式改變了大小。
在阿方讓妻子離開後,阿方認出陌生的來訪者是一個 "圓",是一個在他社會中最備受尊敬的 "圓"。
「哦!這不是一個女人,也沒有任何角度,一點痕跡都沒有。難道我對一個完美的圓形如此失禮嗎?」
而陌生的來訪者說出謎一般的話語
"在某種意義上,我確實是一個圓圈,"聲音回答道,"而且是比平面世界中任何一個圓圈都更完美的圓圈;但更准確地說,我是許多圓圈合而為一。"
當然這是因為三維立體空間的來訪者,是一個 "球"。

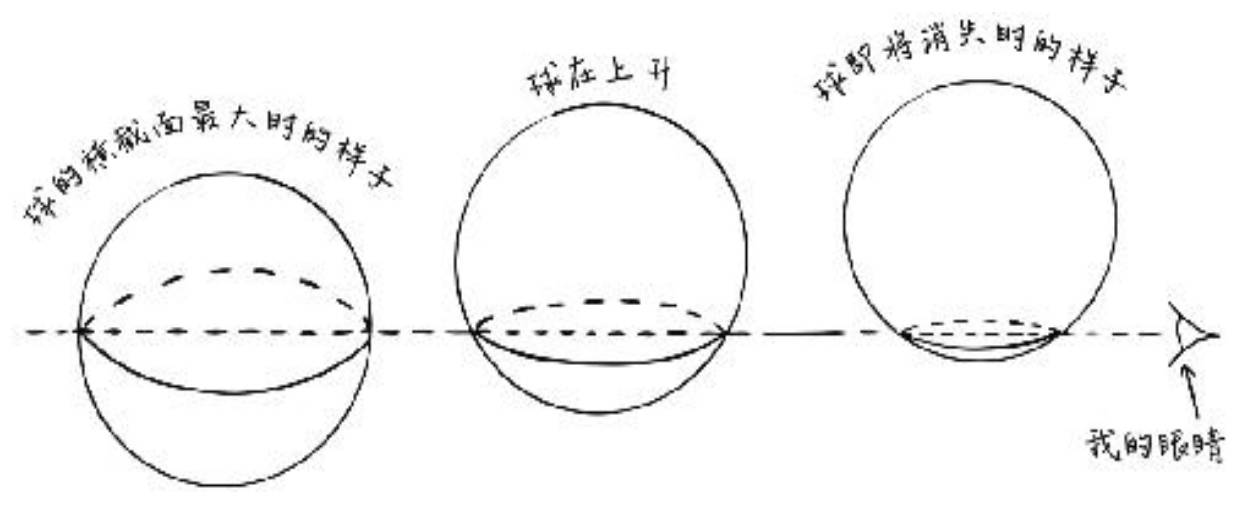
當這個陌生的 "球" "降臨" 在阿方所在的二維空間,那麼阿方就會根據其經驗與學識感知到 "圓",阿方知覺到的 "圓",就是 "球" 在二維平面的截面 (section)。
阿方眼睛感官看到的,是這個 "球" 的二維截面的一維投影,阿方透過對這個一維投影作 "知覺解釋",得出他看到的是一個二維的 "圓"。
我一生中從未遇到過一個更完美的圓。我繞著他走了一圈,他一動不動,從他的眼睛開始,再回到那裡。他完全是個圓,一個完全令人滿意的圓
三維立體訪客的啟示
阿方看到了一個陌生人出現在他的房子裏,而這個陌生人的 "圓度" 比他生平見過的一切 "趨近於圓" 都更 "圓",這讓阿方對來客非常的尊敬崇拜 (在阿方的世界觀價值觀中,趨近於圓即是尊貴)。
阿方︰尊敬的大人,請原諒我的拙劣表現,這並非因為對禮儀不熟悉,而是因為這次有些出乎意料的訪問讓我感到驚訝和緊張。我懇求您不要向任何人透露我的失態,尤其是不要告訴我的妻子。但在閣下進一步交流之前,是否能滿足一位渴望知道閣下來自何方的人的好奇心呢?
球體︰來自空間 (Space),來自空間 (Space),先生,我還能從哪裡來呢?
阿方︰尊敬的大人,請原諒,您的閣下是否已經身處於空間中,您的閣下和他的謙卑僕人,此刻甚至也是如此?
球體:唉!你對空間 (Space) 了解多少?定義一下空間 (Space)。
阿方︰空間,我的主人,是無限延伸的高度和寬度。
球體:正是,你看,你甚至不知道空間是什麼。你認為它只有兩個維度;但我來告訴你第三個維度——高度、寬度和長度。
阿方與三維球體訪客,以某種形式重覆了前一天阿方與一維國王的互動過程。三維訪客嘗試向阿方說明「第三維 - 高度」的存在,而阿方則完全理解不能,到底甚麼是「高度」?
阿方︰閣下是否能指示或解釋給我,第三維度在哪個方向上?這對我來說是未知的。
球體︰我來自它。它在上面 (ανα) 和 下面 (κατα)。
阿方︰大人似乎是指北方和南方。
球體︰我不是指那种意思。我是指一個你無法看到的方向,因為你的身體側面沒有眼睛。
阿方︰尊貴的大人,請原諒我,稍作檢查即可讓閣下確信,我在兩側的交界處擁有一個完美的光源。
球體︰是的,但是要看清楚空间,你应该有一只眼睛,不是在你的周长上,而是在你的侧面,也就是你可能称之为 内部 (εσωτερικός = esoteric = 內) 的地方;但是在空间世界中,我们会称之为你的侧面。
阿方︰我裡面 (εσωτερικός = esoteric = 內) 有一隻眼睛?!我的肚子裡也有一隻眼睛?!閣下開玩笑吧。
這個 "側" 與 "內" 的話題,以另一種形式再現於阿方與球體訪客的對話之中。
然後兩人繼續進行著跨維度的無效溝通。
球體︰不,實際上不是。我所指的「高度」是一個像你的長度一樣的維度:只是對於你們來說,「高度」並不容易察覺,因為它非常小。
阿方︰大人,您的主張很容易驗證。您說我有第三個維度,您稱之為“高度”。現在,維度意味著方向和測量。只要測量一下我的“高度”,或者簡單地告訴我我的“高度”延伸的方向,我就會成為您的信徒。否則,您的尊貴之處必須原諒我的理解。
類同一維國王的 "線性理性" 無法理解二維阿方的啟示,二維阿方的 "平面理性" 也無法理解比他維度高的球體啟示。
在一輪無效的說服後,球體決定進行 "奇蹟" 的實踐,球體將自己的身體往阿方所處的平面 "穿透" 一次。而在阿方的視覺中,就是球體 "變小" 了,然後還 "消失" 了,卻仍然從 "正方形身體內部" 聽到球體的聲音。
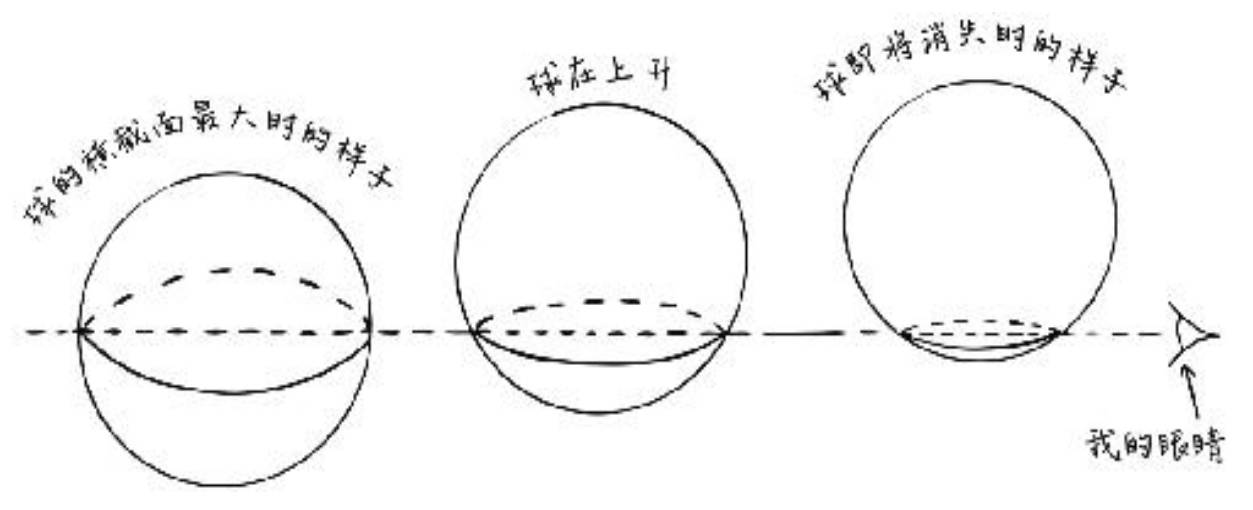
阿方︰但對於我來說,儘管我看到了事實,原因仍然是一片黑暗。我所能理解的只是,這個圓形變得更小並消失了,現在又重新出現並迅速變大。
球體在展現了 "奇蹟" 後,阿方仍然陷入深深的迷惑,於是球體像蘇格拉底一樣,對阿方進行了一輪 "幾何知識助產術",從點開始推導線,由線到面,再嘗試由面的特質,推導到三維立體。
但球體失敗了,阿方不相信經由心智邏輯下數學推導的結果,那個推導出來的結果對阿方來說太詭異、太瘋狂、太異常、太不能接受。於是阿方瘋了,阿方大叫「不管你是魔術師、巫師、夢境還是惡魔,我再也不會忍受你的嘲弄了。你我之間,必有一人必死。」
然後阿方就對啟示者發起了攻擊。
徒勞無功。我將我最堅硬的直角與陌生人猛烈碰撞,用足夠的力量壓迫他,足以摧毀任何普通的圓形:但我能感覺到他慢慢而不可阻擋地從我的接觸中滑落;不向右邊或左邊靠,而是以某種方式離開這個世界,消失得無影無蹤。很快,一片空白。但我仍然聽到入侵者的聲音。

天上來信使,帶來千禧年的三維福音,選中的使徒卻瘋了
球體很失望,他以為阿方作為一個相對公正的人、數學家,儘管有諸多世界觀的限制,有諸多缺陷和偏見,但會能接受自己的心智邏輯推導結果,然而阿方選擇相信的是他眼睛能看到的一維投影。
三維社會的規矩是每過 1000 年,他們派出 信使 (άγγελος = angel = 天使) 向二維社會的人們作出三維的啟示 (Revelation)。
而這次新千禧年剛開始,宣道之路就遇上了重大挫折。三維福音 (ευαγγέλιο = ευ + άγγελος = 好的訊息) 傳不下去。
他們選中的 使徒 (απόστολος = apostle= 負使命者) 雖然能進行心智邏輯的推導,卻不接受邏輯推導的結果。使徒在接受啟示後認為這是妖異之見,瘋狂地攻擊 "天上" 的來使 (άγγελος = angel = 天使)。
球體︰為什麼你不願意聽理性的論點呢?我本以為在你身上——作為一個有理智和卓越數學家的人——我能找到一個合適的使徒,來傳揚每千年才被允許傳講一次的三維福音 (ευαγγέλιο = ευ + άγγελος = 好的訊息) 。但現在我不知道該如何說服你。等等,我有辦法了。行動,而不是言辭,將宣告真理。聽著,我的朋友。
三維的視野並非無漏全知
再經過一大輪無效的 "奇蹟" 演示後,球體絕望了,他決定用最粗暴的方式,將阿方 "震" 出其熟悉的二維平面,讓阿方的眼睛 "目睹" 他的 "三維福音"。
而被 "震" 出二維平面後,阿方終於理解到球體對他的啟示是甚麼,"三維福音" 又是甚麼。
阿方︰我看了,看哪,一個新世界!在我面前站著一個明顯無形的存在,所有我之前推斷、猜測、夢想的完美圓形美麗。
阿方︰再一次,我感到自己在三維空間中升起。正如球體所說的一樣。我們離開所看到的物體越遠,視野就變得越廣闊。我的家鄉城市,每個房子和其中的每個生物,都以微縮的形式展現在我的眼前。我們越往上升,地球的秘密、礦坑的深處和山洞的最深處,都在我面前展露無遺。
阿方認為,他看到這麼不可思議的景象,這是「神」的全知全能。

然而阿方的想法卻被球體反駁。
對地球的神秘景象感到驚嘆,眼前的一切展現在我不值得的眼中,我對我的同伴說:“看哪,我已經成為了神。因為我們國家的智者們說,看到萬物,或者用他們的話來說,全知全能,只有神才具備這種屬性。”
我的導師回答時聲音中帶著一絲輕蔑:“真的嗎?那麼,我的國家裡的扒手和殺人犯也應該被你們的智者們崇拜,因為他們每個人都能看到你現在所看到的一樣多。但請相信我,你們的智者們是錯的。”
在球體看來,三維的視覺既不無知也不無能,三維的視覺只是相對於二維視覺知道得更多,三維世界的人們能隨時俯瞰二維平面的所有細節,這卻不代表三維世界充滿了善人與義人,三維居民只是意識到更多的可能性。
三維的視野,並不等同於善 (ἀγαθός) 的視野,三維只是比二維看到的東西更多,意識到更多的可能性。正如二維容易看到一維看不到的東西,卻不代表二維的阿方是神。只是阿方想的話,他可以對一維世界偽裝成一個 "神",這是二維邏輯對一維邏輯的信息優勢。
球體︰如果我們國家的扒手或殺人犯能看到你們國家的一切,這絕對不是你們應該將他們視為神的理由。你們所謂的全知全能,在空間國度並不常見,這能讓你們更正義 (δικαιοσύνη)、更慈悲、更無私、更有愛心 (caritas) 嗎?一點也不。那麼,它又如何使你們更神聖 (άγιος = holy) 呢?

秩序、城邦、信使的困境
球體對阿方展現他的啟示後,帶著阿方來到二維平國世界的政治核心所在地,這是新的千禧年的開始,2000 年的第一天,國家領袖都集中到一起在開會。
在會議上,平面國的統治者宣佈,每逢千禧年的開始,就會有臣民陷入幻象,宣稱自己接受到來自 "上天" 的啟示,並說一些諸於 "三維世界存在"、"長和寬之外還有一個維度"、"有新世界" 等的話語來妖言惑眾,荼毒年輕人的心智與靈魂,敗壞社會的道德,危害國家的秩序。
如此,圓們指示要嚴格搜查這些迷失方向的人。
看完這些,球體如同他的前人一樣,"降臨" 到平面國的政治核心,向祭司們宣告三維空間的存在。
而首席主圓等最高層的統治者對突然出現陌生人毫不驚訝,因為歷史上也早已發生過這種事,還留有檔案記錄這些事。
「諸位大人,」主席對著委員會的初級成員們說道,「毫無疑問,不需要感到驚訝;只有我能夠進入的秘密檔案告訴我,在過去兩次千年開始儀式上也發生過類似的事情。當然,你們在內閣之外不要提起這些小事。」
首席主圓下令封口,並將現場級別低的人全關起來。
阿方的兄弟也在現場,他是一個正方形的書記員,所以也被關起來了。
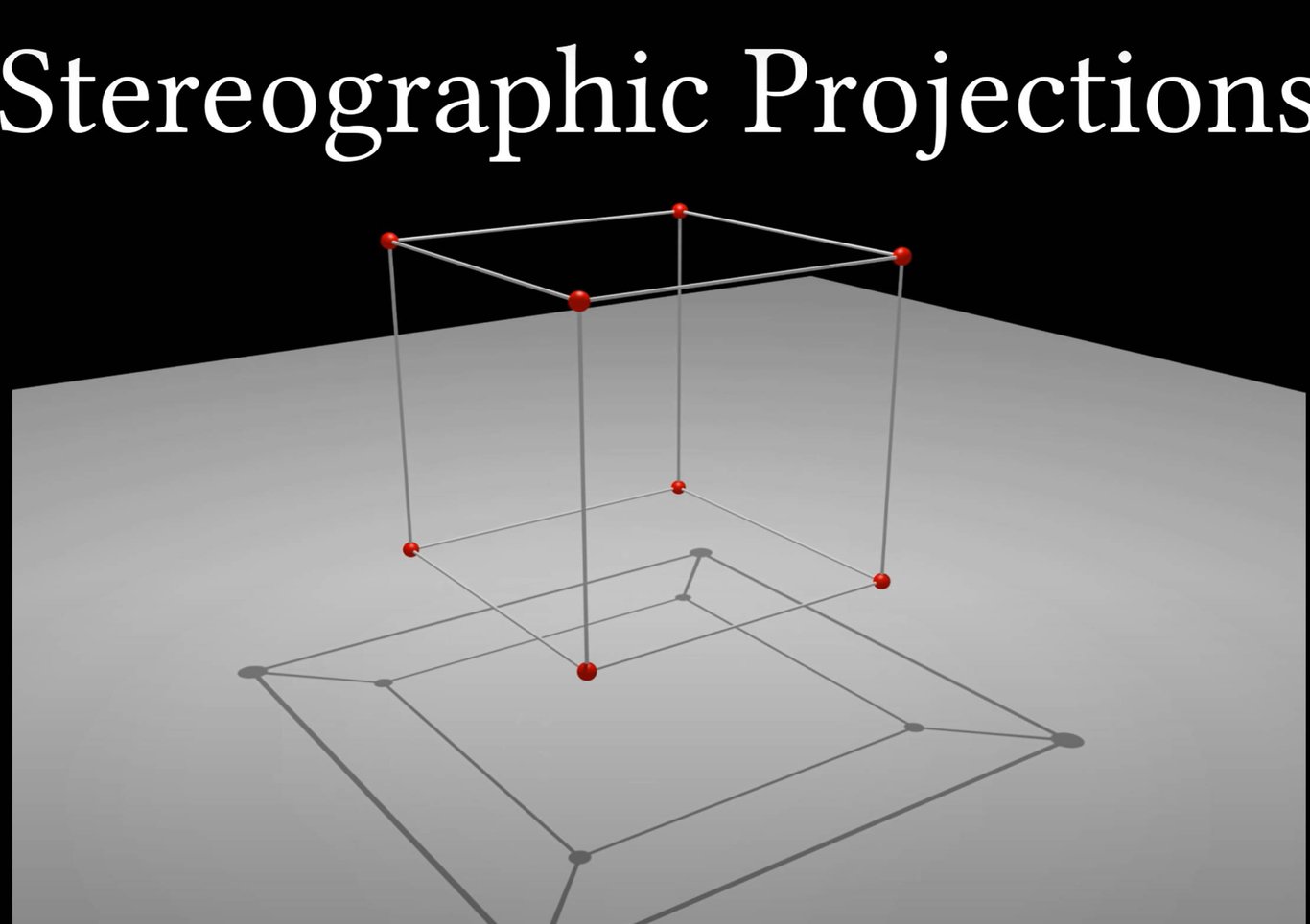
投影、類同、邏輯
球體完成 "降臨" 與 "啟示" 後,繼續教導阿方三維空間的知識,其中包括光線、陰影、視角、透視等的認識。
而經過這些教導,阿方陷入了一種迷醉的喜悅,因為他認識到,按 類同 (αναλογία = analogy) 的 邏輯 (λόγος = logos),三維空間 "之上",還可能存在一個 "四維空間"。
對阿方來說,球體是如此的博學多能,是高維的存在,必定能理解他的邏輯,並且有能力向阿方展示四維空間的宏偉。
沒想到阿方此舉激怒了球體信使,球體認為阿方的邏輯一派胡言,他從未見到過甚麼三維空間之外的另一個維度。
其後他們經過一番周折,到訪了零維的世界,在零維的世界就只一個點,一個存在,而那個零維的存在之外別無他人,他認為自己就是世界,不知道有更廣闊的存在。
到訪零維後,球體向他的學生承認,的確有四維空間存在的可能性。


路過小鎮的旅客記起,Charles Howard Hinton [19] 是把超立方體命名為 tesseract 的人,他寫了一本書叫 The Fourth Dimension [20]。
Dionys Burger 寫了一本受《平面國》啟發的 《球體國》(Sphereland) [21]。

(超過了字數限制,分成了上下兩部)
[1] 希帕蒂婭 (Hypatia / Ὑπατία)
https://en.wikipedia.org/wiki/Hypatia
[2] 《平面國》(Flatland) 原文
https://www.gutenberg.org/files/201/201-h/201-h.htm
[3] https://en.wikipedia.org/wiki/Flatland
[4] https://zh.wikipedia.org/zh-hant/%E5%B9%B3%E9%9D%A2%E5%9C%8B
[5] Edwin A. Abbott
https://en.wikipedia.org/wiki/Edwin_Abbott_Abbott
[6] Flatland 1965
https://www.youtube.com/watch?v=yBbZmwROv84
[7] Flatland (TED)
https://www.youtube.com/watch?v=MGv8MMi8QO0
[8] Flatland (2007) & Flatland2: Sphereland (2012)
https://www.bilibili.com/video/BV14s411y7GK
https://www.bilibili.com/video/BV1Ht411E7cu
[9] Flatland The Film (2007)
https://www.youtube.com/watch?v=avMX-Zft7K4
[10] https://people.math.harvard.edu/~knill/mathmovies/swf/flatland_2to3.html
[11] 臺灣通識網 數學的故事 Tales about Mathematics / 徐惠莉
https://www.youtube.com/playlist?list=PLfS0WrMWEu_47uf3wDOXkVTdycsehWqYI
https://www.youtube.com/watch?v=-IbUDqI2Cq4
[12] https://www.hitl.washington.edu/projects/knowledge_base/virtual-worlds/EVE/III.A.1.c.DepthCues.html
[13] https://en.wikipedia.org/wiki/Perspective_(graphical)
[14] https://www.math.hkust.edu.hk/~yangwang/Course/2016FSMath4999/Weiping%20Li/perspective.pdf
[15] http://vr.theatre.ntu.edu.tw/fineart/th9_1000/open-21-broadcast.htm
[18] 光學錯覺 Optical Illusions
https://www.beautifullife.info/urban-design/10-crazy-3d-optical-illusions-will-blow-mind/
[19] Charles Howard Hinton
https://en.wikipedia.org/wiki/Charles_Howard_Hinton
[20] The Fourth Dimension, Charles Howard Hinton
https://www.gutenberg.org/cache/epub/67153/pg67153-images.html
[21] https://en.wikipedia.org/wiki/Sphereland
(上部完)
喜欢我的作品吗?别忘了给予支持与赞赏,让我知道在创作的路上有你陪伴,一起延续这份热忱!











- 来自作者
- 相关推荐