輕鬆了解zk-SNARK — 第二篇

前言
上一篇 zk-SNARK原理詳解 — 1 中,我大概講了一些零知識證明的概念以及ZCash如何運作的。為什麼使用 ZCash做講解?除了它是一個用零知識證明來處理隱私交易的幣之外,它的文檔對我學習這個知識提供非常多幫助。
另外,我也參考了V神、以及一些大神的文章、論文,整理成一篇我認為大家容易理解的文章(相比於其他文章),希望大家看完後可以跟阿嬤解釋什麼是零知識證明,記得順便帶點靈芝給阿嬤~

抱歉很尬,我們直接開始。
在這篇論文中第 25頁,作者整理出零知識證明的過程中會有哪些運算。

當然,這篇文章不會拿上圖做講解,嚇嚇人而已!接下來正式開始進入講解環節~
這邊很重要
回顧一下 zk-SNARK 的意思,全名為 Zero Knowledge Succinct Non-Interactive Arguments of Knowledge,也就是簡潔的、無交互的零知識證明。
其主體是 Argument of Knowledge(知識證明),也就是說,最重要的是驗證者所生成的證明,此證明與挑戰者所提出的問題相對應。
其實這個觀念與其他不同的證明法是一樣的,但困難之處在於
- zk(零知識),具體一點就是 — 在交易中,你必須證明你擁有某種未花費的資產,但是不想暴露資產的來源、去向。
- Succint(簡潔的),驗證過程中生成的資料大小以及驗證時間都要小於直接暴力運算,因此我們不能讓驗證者每輪都做 hash運算(否則就跟計算量成正比了)。
- Non-Interactive(無交互),沒有交互是要驗證啥?
關於這些操作是如何完成的,且聽我娓娓道來~
哦對,為了讓大家知道我們進行到哪個步驟了,我用羊皮紙來追蹤我們的進度,夠誠意了吧!
本文中,我們會一直看到這張圖,看到你做夢都記得…
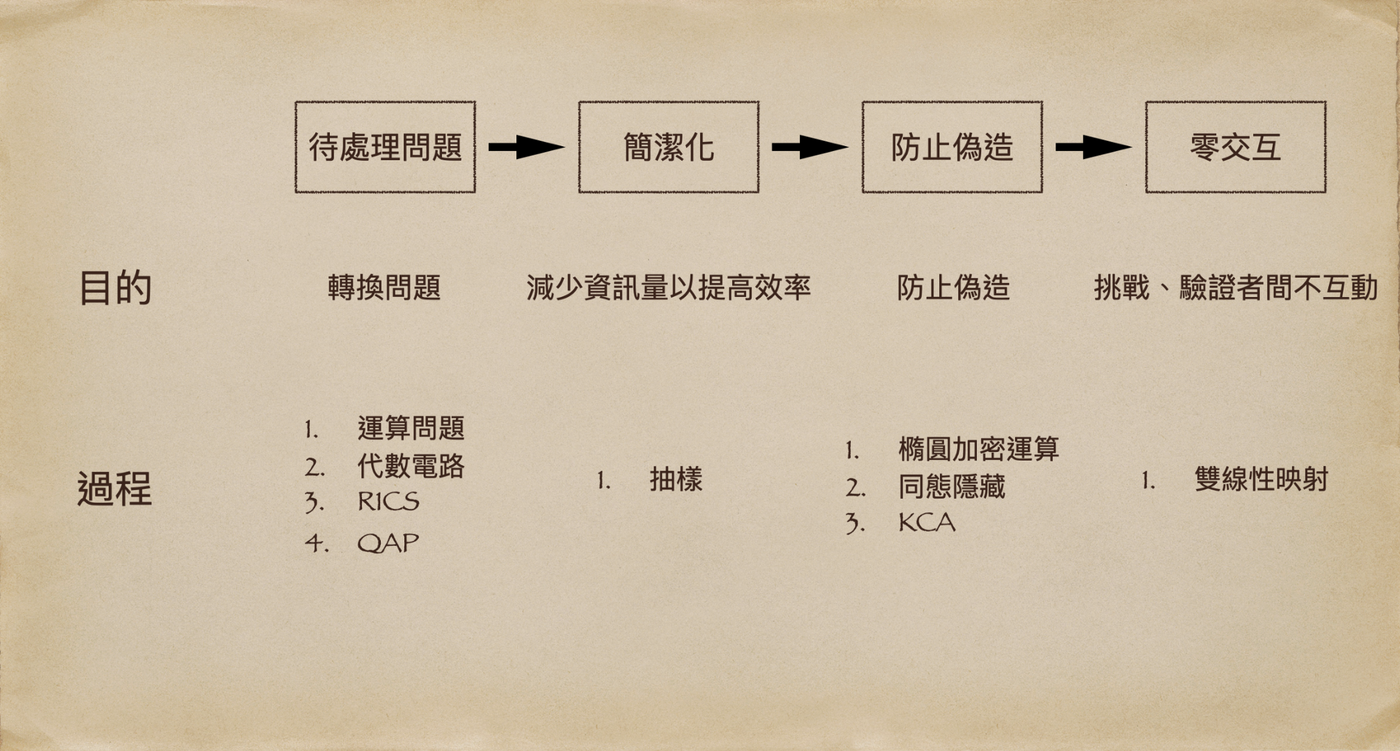
我們先來取得一個共識…
程式在處理的就是將輸入值運算,zk-SNARK作為一種數學證明,若要能用程式處理,就要有可量化的輸入值,而要進行運算之前,必須先為目標問題建立出一個模型(此模型包含上圖中所有的進行動作),有了模型以及輸入值,才能得到想要的結果。
再說得白話一點,我們在選取問題的特定輸入值後,代入我們所建立的 function後,可以得到一個解,在 zk-SNARK中這個解叫做證明,用來證明驗證者的確知道這個解。
有了這個共識後,再來進行下一步。
進行證明前,先轉換為成適當的格式 — QAP
如前一段所述,我們要建立一個模型以進行零知識證明,既然是模型,就要能涵蓋到大部分的傳入值,不能出現有些可以、有些不行的情況,也因為我們明白:
- 並不是任意運算問題都可以進行 zk-SNARK
- NP問題的所有實例都可以在 zk中被證明
第一點其實蠻直觀的,關於第二點,在這則論文中解釋了所有NP問題都有零知識證明。
小百科:一般問題可分成兩類: P問題 和 NP問題 。P問題指的是在多項式時間內可解 的問題。 NP問題(Non-Deterministic Polynomial Problem,非確定性多項式問題),指不能在多項式內可解,但是可以在多項式時間內驗證 的問題。
基於上述兩點,我們應該確保傳入模型執行 zk-SNARK的傳入值是 NP問題,而且是可以在模型中被運算的形式。
在 zk-SNARK中,這個轉換的最終結果是QAP(Quadratic Arithmetic Program),如何轉換以及轉換的邏輯會在稍後說明,現在只需要先了解下面那張圖就好了
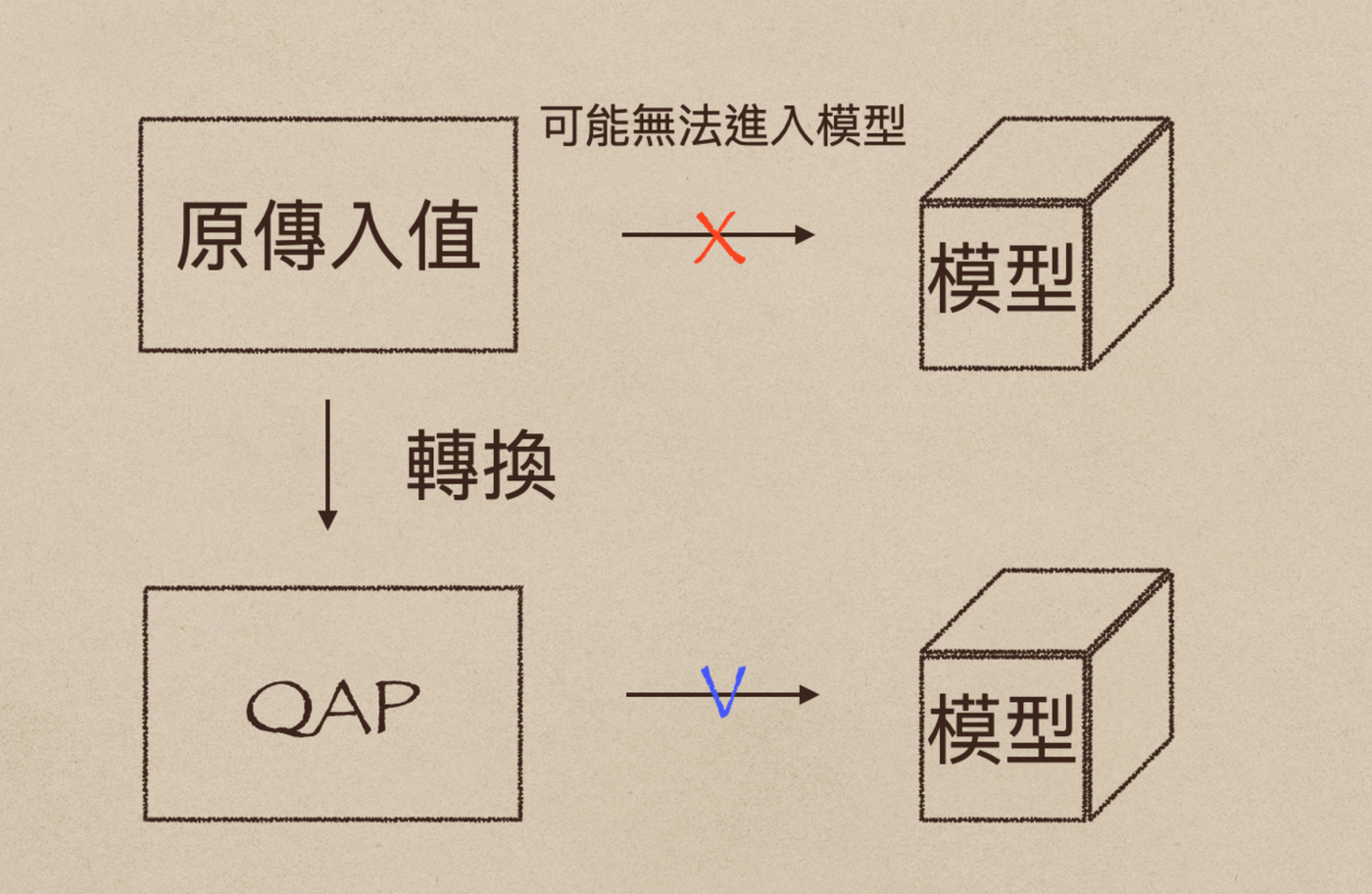
總而言之,我們需要輸入值呈現一個正確的格式來執行後續運算,這個格式在zk-SNARK中就是QAP。我們也因此把zk-SNARK拆成兩個部分。
- 將初始輸入值轉換為QAP
- 進行後續運算
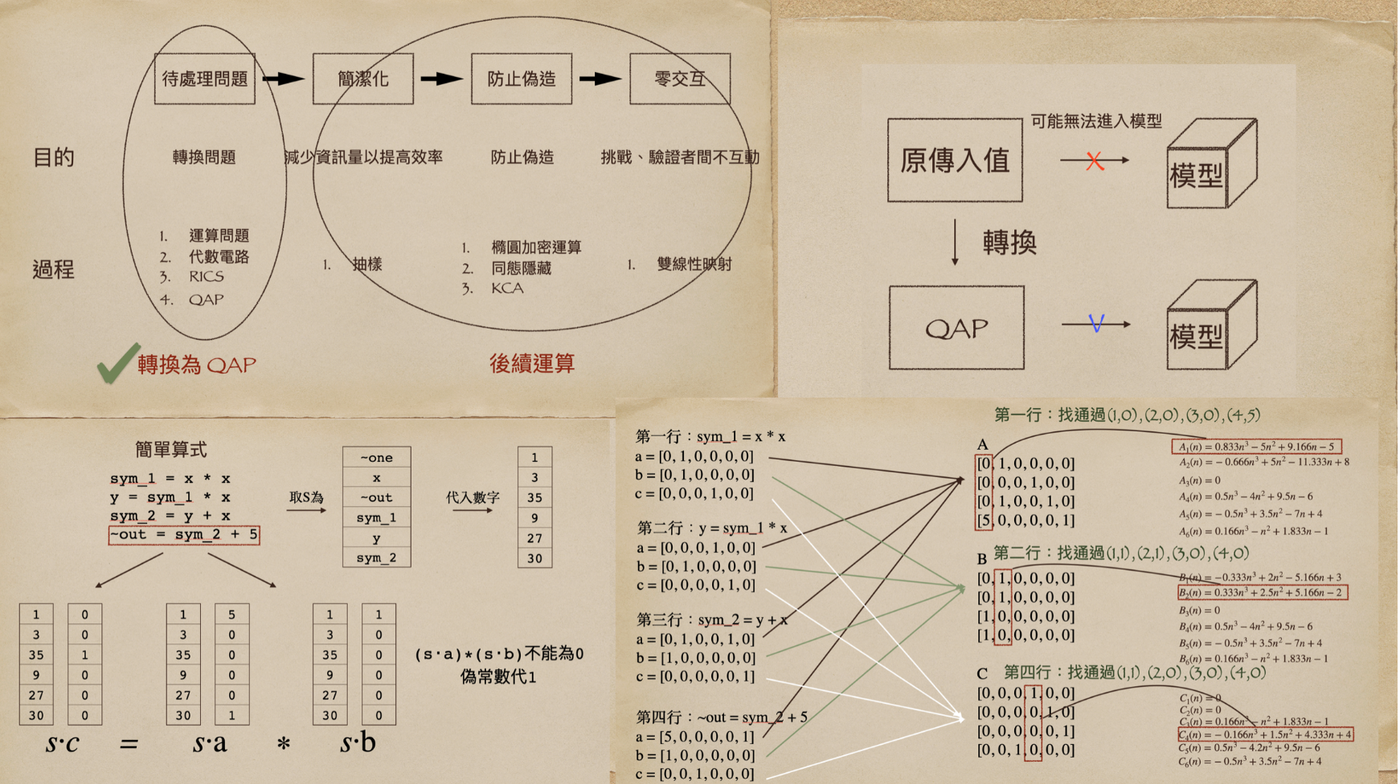
於是現在流程圖長這樣了~
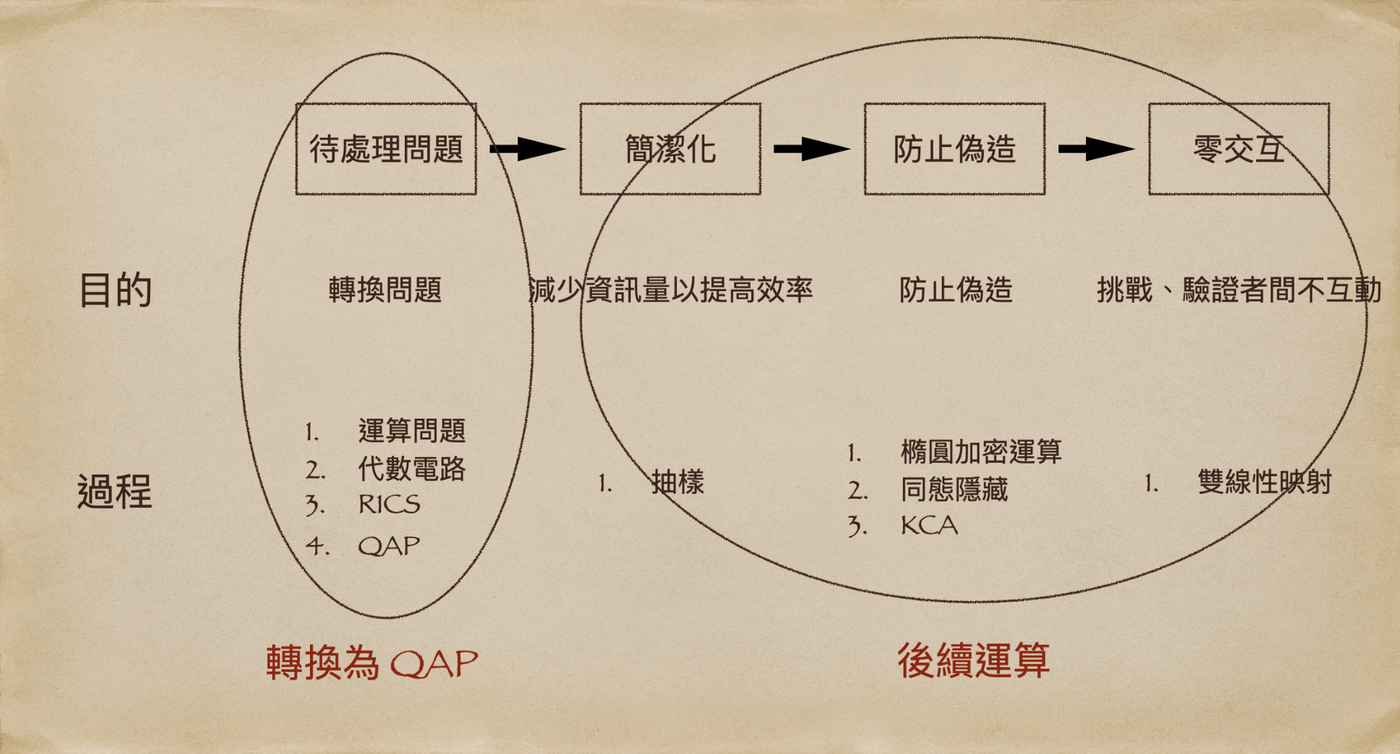
本文主要會講解第一部分 — 轉換為 QAP,第二部分留到之後的文章。
一直說QAP QAP,但它是什麼?又是怎麼轉換的?
QAP轉換過程
我們以V神文章中所提供的範例舉例,這個過程中我們要去證明我們知道 x³+x+5=35 的解,但這個例子可以讓我們理解zk-SNARK的技術原理,同時又不會產生很大的 QAP。
x³+x+5=35如下:
def qeval(x):
y = x**3
return x + y + 5
轉換為QAP的主要目的
稍後我們會進行三個步驟將一個函數轉換成 QAP,QAP是以多項式的形式表示,然而為什麼要費盡心思弄出多項式,其實是為了滿足後續以「抽樣」來實現「簡潔」,但這就是下一篇的內容啦,現在做這個聲明只是先跟讀者說明我們要轉換的原因,現在讓我們繼續跑完流程吧!
過程主要分為三個步驟
1.引入變數
將 x³+x+5轉換成幾個簡單算式,例如 x=y, x=y(op)z這種形式,op(operation) 代表加、減、乘、除,這些簡單算式可以視為數位電路中的邏輯閘,也因此被稱為代數電路(Algebraic Circuit)。
sym_1 = x * x y = sym_1 * x sym_2 = y + x ~out = sym_2 + 5
上式中,sym_1, y, sym_2就是我們所引入的變數,將 x=3, sym_1=9, y=27, sym_2=30, ~out=35代入其中,等式成立。
這種轉換的過程有另一個名詞叫做 flattening(拍平),拍平後的每一個式子其實都是一個邏輯閘。
2.定義向量
定義向量s=[~one, x, ~out, sym_1, y, sym_2],其中~one為偽變量,實際上是常數 1,這個偽變量的作用稍後就會看到了。

將每個我們轉換過的簡單算式再轉換為(s⋅a)∗(s⋅b)−(s⋅c)=0,其中 ⋅ 為向量內積運算子,a,b,c為係數向量。
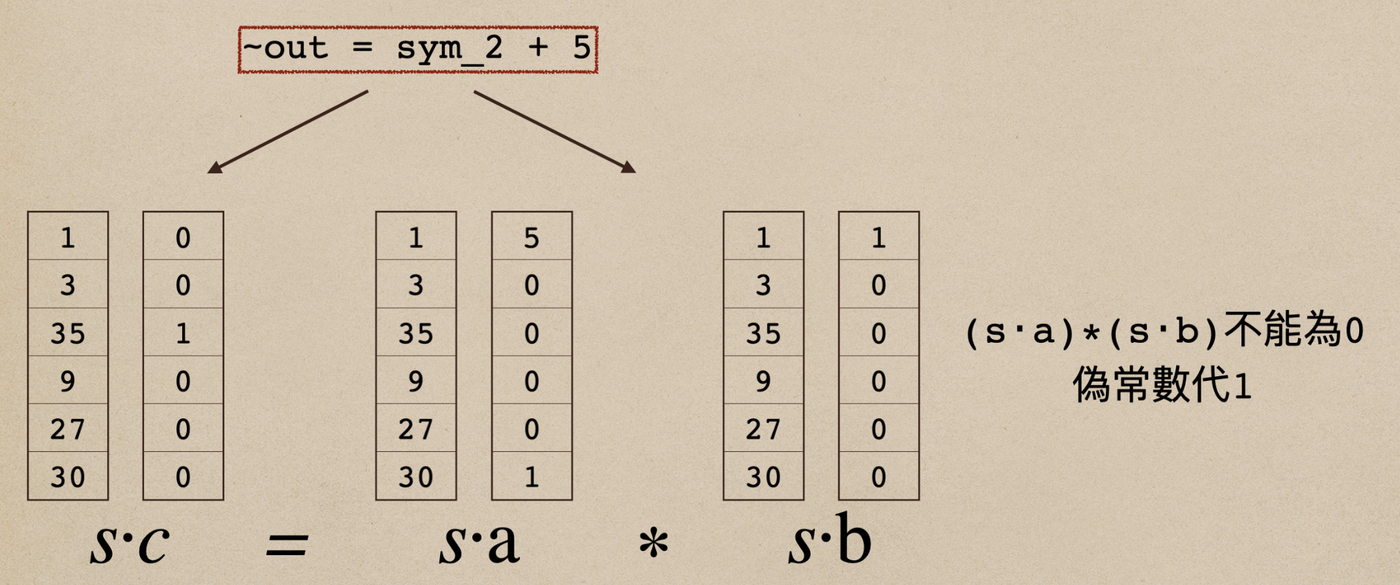
要了解找 s與 a, b, c的原因,就要先了解什麼是 R1CS(Rank-1 Constraint System,一階約束系統) 。
R1CS 是由三向量組 (a,b,c) 組成,R1CS 有個解向量 s,s 必須滿足(s⋅a)∗(s⋅b)−(s⋅c)=0。這裡的解向量 s就是 witness。上例中:
s = [1, 3, 35, 9, 27, 30]
a = [5, 0, 0, 0, 0, 1]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 1, 0, 0, 0]
複習一下,上面的動作是在將最後一個邏輯閘(“拍平”後的最後一個式子) 轉換成一個約束(即一個三向量組)。
接下來我們再將剩下三個邏輯閘做相同操作找出各自 a,b,c向量
sym_1 = x * x y = sym_1 * x sym_2 = y + x ~out = sym_2 + 5 我們已經完成這行

將係數向量依順序排列(各行所得到的 a, b, c集合起來),得到A, B, C三矩陣。
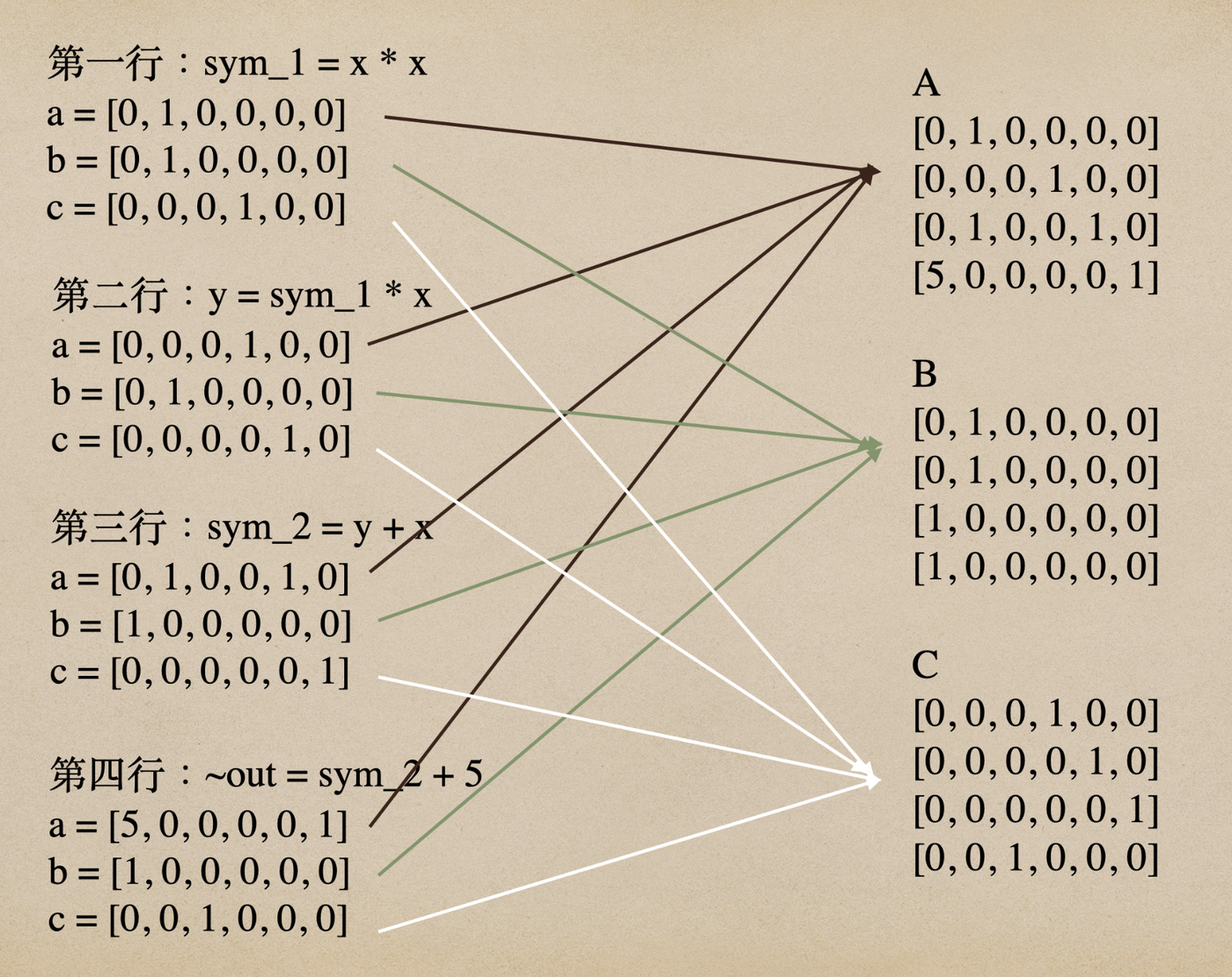
至此第二個步驟完成!
第三個步驟,我們要做的是將 R1CS轉換成 QAP形式
補充:
R1CS與 QAP所要實現的邏輯完全相同,兩者的區別在於 QAP使用多項式來代替內積運算。
在介紹這種轉換之前,我們需要複習拉格朗日差值公式,這個公式的作用是建立一個穿過指定點的多項式,相信各位在國高中也都有學過
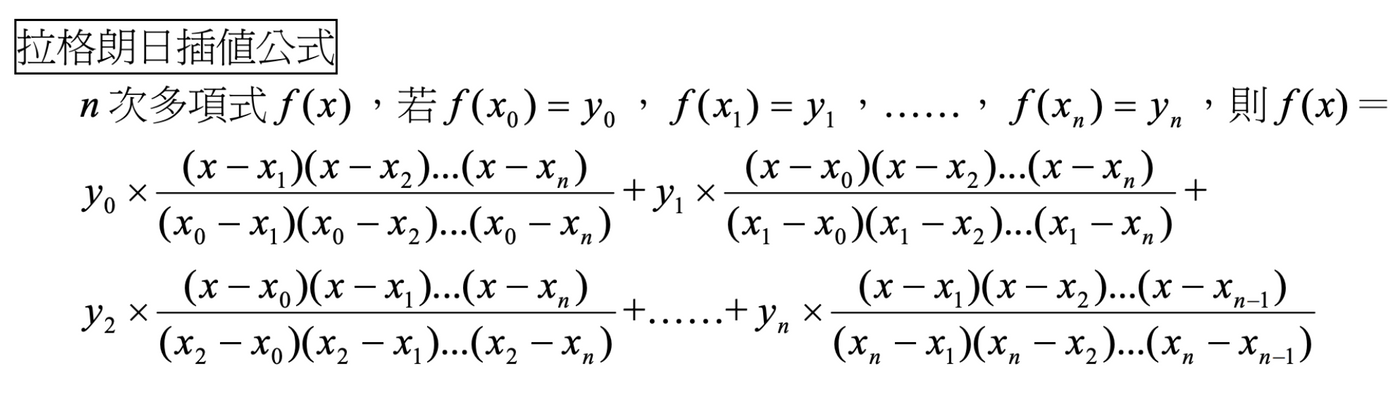
例如通過點 (1,3), (2,2), (3,4) 的多項式為:
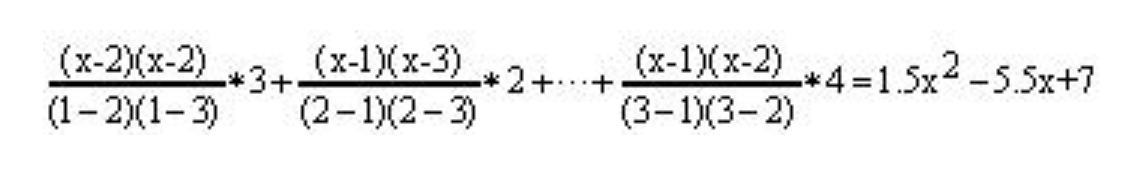
前面提到,第三個步驟的目的是把 R1CS轉換為 QAP,使用的就是拉格朗日差值公式。
這個步驟,比較像是在壓縮矩陣,因此我們的第三個步驟就稱作壓縮矩陣。
3. 壓縮矩陣
現在我們要來將 A, B, C三個矩陣分各自轉換為六組多項式。
概念大概是這樣:
矩陣C → C(n)=[C1(n), C2(n), C3(n), C4(n), C5(n), C6(n)]
每組多項式包括三個三階多項式,我們在每個 x點處來評估不同的約束,在這裡,我們共有四個約束,因此我們分別用多項式在 x = 1, 2, 3, 4 評估這四組向量組。
我們先求出四個約束所對應的每個 a 向量的第一個值的多項式,也就是說,使用拉格朗日插值定理求過點 (1,0), (2,0), (3,0), (4,0) 的多項式,類似的我們可以求出其餘的四個約束所對應的每個向量的第 i 個值的多項式。結果如下:

在得到這些多項式後,計算問題就轉換成求 s (s是解向量,一開始有提到),使 (s⋅a)∗(s⋅b)−(s⋅c)=0 在 n = 1,2,3,4,5,6 成立,也等價於:
[s⋅A(n)]∗[s⋅B(n)]−[s⋅C(n)]= H(n)*Z(n),其中Z(n)=(n-1)(n-2)(n-3)(n-4)(n-5)(n-6)
至此,我們終於得到一個涵蓋全部的多項式,也就完成第一部分了!
沒想到光第一部分畫圖就畫這麼久,下一篇我們開始講解後續運算。
歡迎留言或是 email: [email protected] 一起討論
或是追蹤本帳號獲得新文章通知!
參考資料
How Transactions Between Shielded Addresses Work - Electric Coin Company
Introduction to zkSNARKs with Examples
A practical overview of zk-SNARKsmedia.consensys.net
Quadratic Arithmetic Programs: from Zero to Hero
